Вычисление объемов тел вращения

Пусть на отрезке[ a, b ] задана непрерывная знакопостоянная функция y=f(x). Объемы тела вращения, образованного вращением вокруг оси Ох (или оси Оу) криволинейной трапеции, ограниченной кривой y=f(x) (f(x) 0) и прямыми у=0, х=а, х=b, вычисляются соответственно по формулам:

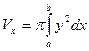, ( 19 )

(20)

Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривой и прямыми x=0, y=c, y=d, то объем тела вращения равен

. (21)

Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг оси Ох.

По формуле (19) искомый объем

(ед.²)

Пример. Пусть в плоскости xOy рассматривается линия y=cosx на отрезке .

Эта линия вращается в пространстве вокруг оси 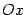, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объём этого тела вращения.

Согласно формуле, получаем:

Площадь поверхности вращения

Если дуга кривой, заданная неотрицательной функцией , , вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле , где a и b — абсциссы начала и конца дуги.

Если дуга кривой, заданная неотрицательной функцией , , вращается вокруг оси Oy, то площадь поверхности вращения вычисляется по формуле

,

где с и d — абсциссы начала и конца дуги.

Если дуга кривой задана параметрическими уравнениями , , причем 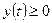, то

Если дуга задана в полярных координатах , то

.

Пример. Вычислим площадь поверхности, образованной вращением в пространстве вокруг оси 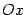части линии y= , расположенной над отрезком оси .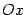

Так как , то формула даёт нам интеграл

Сделаем в последнем интеграле замену t=x+(1/2) и получим:

В первом из интегралов правой части сделаем замену z=t²- :

Для вычисления второго из интегралов в правой части обозначим его и проинтегрируем по частям, получив уравнение для :

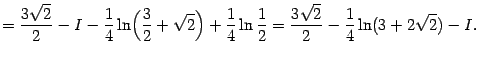
Перенося в левую часть и деля на 2, получаем

откуда, наконец,

Дата добавления: 2015-10-30