Практическая оценка погрешности при применении квадратурных формул

В полученные нами формулы оценки ошибки квадратурной формулы входят величины Mk, ограничивающие абсолютную величину производной порядка от подынтегральной функции ( для формул центральных прямоугольников и трапеций, 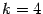для формулы Симпсона, и для формулы Уэддля). Если величина M_k неизвестна (а как правило, в достаточно сложных задачах не вычисление интегралов она неизвестна или получить её весьма нелегко), то пользоваться этими оценками для определения величины ошибки конкретного вычисления невозможно. Так что всё, что дают нам формулы оценки ошибки — это порядок квадратурных формул. Однако на этом основании можно получить следующее практическое правило, которое позволяет получить оценку ошибки конкретного вычисления, если квадратурную формулу применить два раза с разными шагами .

А именно, если используемая квадратурная формула имеет порядок точности ( — порядок формул центральных прямоугольников и трапеций, 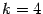— формулы Симпсона, — формулы Уэддля), то соответствующая шагу погрешность имеет оценку , где — некоторая постоянная, не зависящая от . Таким образом, при малых , то есть при достаточно большом числе отрезков разбиения , будет

и

Следовательно, если 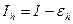— приближённое значение интеграла, точное значение которого равно , то

Отсюда получаем, что

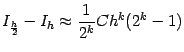
и

(5)

Таким образом, проведя вычисления по данной квадратурной формуле с некоторым шагом , а затем удвоив число отрезков деления и проведя вычисления по той же формуле с шагом 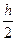, мы получим приближённые значения I_h и I и сможем, применив формулу (5), вычислить текущую погрешность, то есть оценку отклонения истинного значения интеграла от последнего из вычисленных приближённых значений (полученного с шагом ).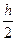

На такой оценке текущей погрешности, как правило, основаны компьютерные программы, вычисляющие значение определённого интеграла с заданной точностью.

Пример. Вычислить интеграл по формуле Ньютона — Лейбница и по приближенным формулам прямоугольников, трапеций и Симпсона, разбивая интервал на 8 равных частей. Оценить в процентах погрешность результатов, полученных по приближенным формулам.

Решение. По формуле Ньютона — Лейбница

.

Делим интервал интегрирования [1;9] на 8 равных частей, находим длину одной части

,

точки деления x_i, значения y_i подынтегральной функции 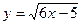в этих точках:

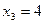
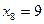
и вычисляем интеграл по приближенным формулам.

1. По формуле прямоугольников:

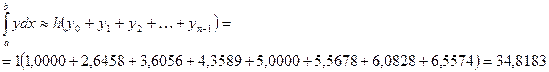(1)

(1а)

Абсолютная ошибка значений равна:

для (1) (по недостатку)

,

для (1а) (по избытку)

.

Относительная (процентная) ошибка:

для (1)

,

для (1а)

.

Погрешность формулы прямоугольников

,

где 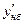— наибольшее значение в интервале [a,b]:

, , .

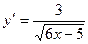2. По формуле трапеций:

Абсолютная ошибка этого результата составляет

,

а относительная

.

Погрешность формулы трапеции

,

где — наибольшее значение в интервале [a,b]:

, , .

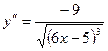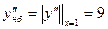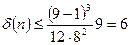3. По формуле Симпсона (n — число четное):

Абсолютная ошибка составляет всего 0,0345, а относительная

.

Погрешность формулы Симпсона

,

где — наибольшее значение в интервале [a,b]:

, , .

---

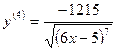Дата добавления: 2015-10-30