Задания для самостоятельного решения

Вычислить интеграл по формуле Ньютона — Лейбница и по приближенным формулам прямоугольников, трапеций и Симпсона, разбивая интервал на 8 (для вариантов 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30) и 10 (для вариантов 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29) равных частей. Оценить в процентах погрешность результатов, полученных по приближенным формулам.

1.

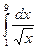
2.

3.

4.

5.

6.

7.

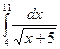
8.

9.

10.

11.

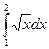
12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

Тест 1

1. При каких а и b функция 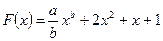является первообразной для

2. При каких целых а, b, c функция является первообразной для функции

При каких целых а, b, c функции и является первообразными для одной и той же функции f(x)?

4. Найти

Ответ: где а, b, d – целые числа: а = …, b = …, d = ….

5. Найти

Ответ: где а, b, d – целые числа: а = …, b = …, d = ….

6. Найти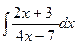

Ответ: где а, b, d – целые числа, дробь несократима, а = …, b = …, d = ….

7. Найти

Ответ: где а, b, d – целые числа, дробь а/b - несократима, а = …, b = …, d = ….

8. Найти

Ответ: где а, b, d – целые числа: а = …, b = …, d = ….

9. Найти

Ответ: где а, b, d – целые числа, а = …, b = …, d = ….

10. Найти

Ответ: где а, b, d – целые числа, а = …, b = …, d = ….

Тест 2

1. Найти максимальное значение интегральной суммы функции у = на отрезке [0, 1] ,если число отрезков разбиения равно 4.

Ответ: a / b, где a = …, b = … (a и b – положительные целые числа, дробь a / b – несократима).

2. При каких целых значениях параметров a и b справедливо равенство ?

Найти такие целые значения a и b, при которых справедливо равенство:.

Вычислить определённый интеграл.

Ответ: , где а = …, b = …(a и b – целые числа).

При каком значении параметра а интеграл dx равен площади S фигуры, ограниченной линиями.Найти эту площадь S.

Ответ: а = …, S = 9 – ln b, где b = … (a и b - целые числа).

Найти длину дуги кривой на отрезке [1,4].

Ответ: a / b, где a = …, b = … (a и b – положительные целые числа, дробь a / b – несократима).

Найти объем тела, полученного при вращении вокруг оси абсцисс плоской фигуры, ограниченной линиями.

Ответ: аπ /3, где а = ….

При каком минимальном значении n формула трапеций обеспечивает вычисление определенного нтеграла с точностью до 0,001?

9. Найти площадь фигуры, заключенной между кривой и ее горизонтальной асимптотой на промежутке [0; +∞).

Вычислить определенный интеграл,если он сходится.

Тест 3

I Интегрирование по частям

1.
2.
3.
4.
5.
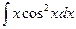
6.
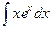
7.
8.
9.
10.
11.
12.
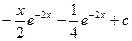
13.
14.
15.
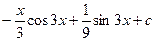
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
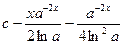
26.
27.
28.
29.
30.

II Иррациональные функции

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
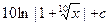
13.
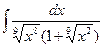
14.
15.
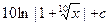
16.
17.
18.
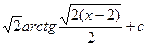
19.
20.
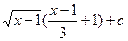
21.
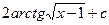
22.
23.
24.
25.
26.
27.
28.
29.
30.

III Универсальная подстановка

1)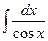
2)
3)
4)
5)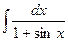
6)
7)
8)
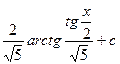
9)
10)
11)
12)
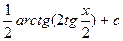
13)
14)
15)
16)
17)
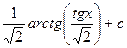
18)
19)
20)
21)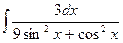
22)
23)
24)
25)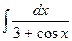
26)
27)
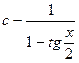
28)
29)
30)

IV Дифференциальный бином

1.
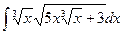
2.
3.
4.
5.
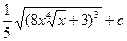
6.
7.
8.
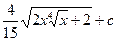
10.
11.
12.
13.
14.
15.
16.
17.
18.
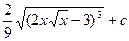
19.
20.
21.
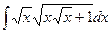
22.
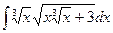
23.
24.
25.
26.
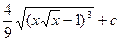
27.
28.
29.
30.

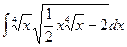
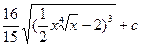
V. Вычислить площадь фигуры, ограниченной линиями (в декартовой системе координат)

1)
2)	y=4-x^2 , y=0
3)
4)
5)
6)
7)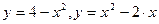
8)
9)		4/3
10)
11)		64/3
12)		4/3
13)		2/3
14)
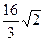
15)
16)
17)	17)
18)
19)		8/3
20)		e-1
21)
22)		8/3
23)		e-1
24)
25)		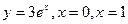3e-3
26)
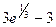
27)
28)
29)
30)		2(e-1)

VI Вычислить площадь фигуры, ограниченной линиями (в полярной системе координат)

1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
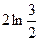
16)
17)
18)
19)
20)
21)
22)
23)
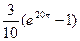
24)
25)
26)
27)
28)
29)
30)

Дата добавления: 2015-10-30