Вычисление площадей, длин дуг и объемов с помощью определенного интеграла

(21) Вычисление площади криволинейной трапеции, ограниченной графиком непрерывной функци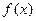и , и прямыми

(22) Вычисление площади криволинейной трапеции, ограниченной графиком функции, заданной в параметрической форме

(23) Вычисление площади криволинейного сектора, ограниченного графиком непрерывной функции и лучами (в полярных координатах):

(24) Вычисление длины дуги кривой, заданной непрерывной функцией 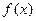, имеющей непрерывную производную, :

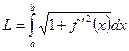
(25) Вычисление длины дуги кривой, заданной функцией в параметрической форме

(26) Вычисление длины дуги кривой, заданной функцией , имеющей непрерывную производную в области определения

(27) Вычисление объема тела вращения, образованного криволинейной трапецией, ограниченной графиком непрерывной неотрицательной функции и прямыми при вращении вокруг оси ОХ:

(28) Вычисление объема тела через площадь поперечного сечения , перпендикулярного оси ОХ:

(29) Вычисление площади поверхности тела вращения, образованного графиком непрерывной, имеющей непрерывную производную, неотрицательной функции 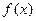при вращении вокруг оси ОХ в области определения :

(30) Вычисление площади поверхности тела вращения, образованного графиком функции, заданной в параметрической форме

(31) вычисление площади поверхности тела вращения, образованного графиком непрерывной, имеющей непрерывную производную, функции в области определения , при вращении вокруг оси ОХ:

Несобственные интегралы

Несобственные интегралы 1-го рода

(1) Если 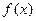непрерывна при 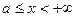, то несобственным интегралом по бесконечному промежутку называют

(2) Если 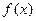непрерывна при , то

(3)

(4) . При интеграл существует (сходится), при интеграл расходится

(5) признак сходимости и расходимости несобственных интегралов 1-го рода (признак сравнения): есл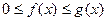и при 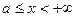, то из сходимости 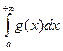следует сходимость 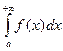, из расходимости 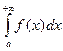следует расходимость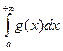

Дата добавления: 2015-10-30