
|
Читайте также: |
Рассмотрим интеграл вида
 , (11.1)
, (11.1)
где 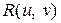 – рациональная функция переменных
– рациональная функция переменных  . Выделяя под корнем полный квадрат трехчлена
. Выделяя под корнем полный квадрат трехчлена  и делая соответствующую линейную замену, интеграл вида (8.1) всегда можно свести к одному из интегралов
и делая соответствующую линейную замену, интеграл вида (8.1) всегда можно свести к одному из интегралов
 .
.
Для каждого из полученных интегралов существуют так называемые тригонометрические подстановки, позволяющие свести их к интегралам от тригонометрических функций.
Для интеграла
 (11.2)
(11.2)
удобна подстановка  . Тогда
. Тогда  ,
,  . В результате этой подстановки получается в общем случае интеграл, подынтегральная функция которого содержит синусы и косинусы. Для его нахождения можно воспользоваться результатами предыдущих параграфов. Найдя интеграл, необходимо перейти от переменной
. В результате этой подстановки получается в общем случае интеграл, подынтегральная функция которого содержит синусы и косинусы. Для его нахождения можно воспользоваться результатами предыдущих параграфов. Найдя интеграл, необходимо перейти от переменной  к переменной
к переменной 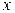 , если учесть, что
, если учесть, что  . Заметим, что здесь подойдет также подстановка
. Заметим, что здесь подойдет также подстановка  .
.
Для вычисления интеграла
 (11.3)
(11.3)
удобно применить подстановку  (
(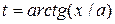 ). Тогда
). Тогда  ,
,
 . Здесь интеграл (11.3) также преобразуется в интеграл от тригонометрических функций.
. Здесь интеграл (11.3) также преобразуется в интеграл от тригонометрических функций.
Для вычисления интеграла
 (11.4)
(11.4)
применяется подстановка  . Тогда
. Тогда 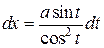 ,
,  .
.
Интеграл (11.4) преобразуется в интеграл от тригонометрических функций.
Следует заметить, что после вычисления интеграла по переменной  всегда необходимо вернуться к старой переменной
всегда необходимо вернуться к старой переменной 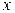 , для чего применяются формулы, выражающие тригонометрические функции через переменную
, для чего применяются формулы, выражающие тригонометрические функции через переменную 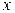 и соответствующие выражения
и соответствующие выражения  ,
,  ,
, 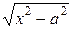 .
.
Пример 1. Вычислить интеграл 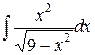 .
.
Решение: Исходный интеграл относится к интегралам вида (11.2). Используем подстановку  (
( ). Тогда
). Тогда




Пример 2. Вычислить  .
.
Решение: Этот интеграл относится к интегралам вида (11.3), так как содержит радикал  . Сделаем подстановку
. Сделаем подстановку  . Имеем
. Имеем
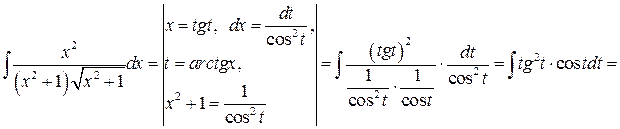

Вернемся к переменной 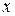 . Учитывая, что
. Учитывая, что  , получим
, получим  . Далее так как
. Далее так как  , то
, то 
 . В итоге
. В итоге

 .
.
В некоторых случаях интегралы (11.1) от иррациональных функций при помощи специальных подстановок сводятся к интегралам от рациональных функций (см. таблица 11.1).
Таблица 11.1.
| Тип интеграла | Способ интегрирования | |
| 1. |  , , 
| Подстановка Эйлера 
|
| 2. |  , , 
| Подстановка Эйлера 
|
| 3. |  , ,

| Подстановка Эйлера 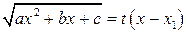 или или 
|
Дата добавления: 2015-10-30; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Схема интегрирования рациональной дроби | | | Формула Ньютона-Лейбница |