Рациональные дроби. Простейшие дроби, их интегрирование

Напомним, что рациональной функцией (рациональной дробью) называются отношение двух многочленов и степеней и :

(, ). (6.1)

Рациональная дробь называется правильной, если 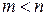и неправильной, если . Если рациональная дробь является неправильной, то ее можно единственным образом представить в виде

, (6.2)

где , 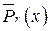– многочлены степеней и соответственно, – правильная рациональная дробь ().

Равенство (6.2) для неправильной рациональной дроби можно получить, если разделить столбиком многочлен на многочлен 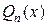, в результате чего выделятся неполное частное и остаток ().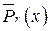

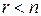Пример 1. Представить рациональную дробь в виде многочлена и правильной рациональной дроби.

Решение: Дробь является неправильной рациональной дробью (, ). Разделим столбиком числитель дроби на знаменатель . Получим:

Тогда , и по формуле (6.2) получим

,

где – правильная рациональная дробь.

Таким образом, из выше сказанного следует, что необходимо рассматривать только правильные рациональные дроби.

Среди правильных рациональных дробей выделяют так называемые простейшие дроби:

I тип: , ,

II тип: , ,

III тип: , ,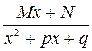

IV тип: , .

Условие для простейших дробей третьего и четвертого типов говорит о том, что квадратный трехчлен 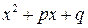нельзя разложить на линейные множители 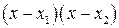, где 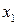, – корни уравнения . Например, рациональные дроби 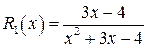, не являются простейшими дробями третьего и четвертого типов, так условие не выполняется (многочлен 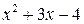можно разложить на линейные множители ).

Рассмотрим схемы интегрирования простейших дробей.

Первый тип простейших дробей интегрируется следующим образом (подводится под табличный интеграл ):

.

Второй тип простейших дробей интегрируется следующим образом (подводится под табличный интеграл ):

.

Интеграл от простейшей дроби третьего типа (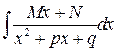) имеет тот же самый вид, что и интеграл (27.3). Поэтому к нему можно применить алгоритм предыдущего параграфа. Выделим полный квадрат трехчлена в знаменателе: 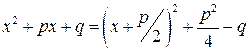. Обозначив , , получим

.

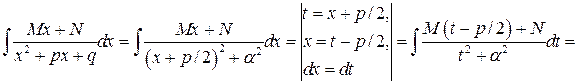
Интеграл от простейшей дроби четвертого типа покажем на примере при 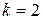. Используя выше введенные обозначения, получим

.

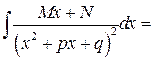
Вычисляем интеграл методом замены переменной

.

Вычисляем интеграл .Учитывая, что , получим

.

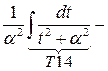
Оставшийся интеграл 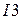находим методом интегрирования по частям.

.

Чтобы записать полностью ответ, необходимо собрать вместе вычисленные интегралы .

Дата добавления: 2015-10-30