Интегрирование некоторых иррациональных

Функций

При интегрировании иррациональных функций главным образом используются замены, которые устраняют иррациональность и сводят подынтегральное выражение к рациональному виду.

1. а) Если подынтегральное выражение содержит лишь линейную иррациональную вида 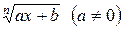, то применим подстановку: .

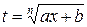б) Если подынтегральное выражение содержит несколько корней с разными показателями степени и с одинаковыми линейными подкоренными выражениями, то необходимо ввести такую замену, после применения которой от иррациональности избавимся (т.е. степень вводимой новой переменной должна быть равной наименьшему общему знаменателю всех дробных показателей).

Пример 2.5.1. Найти .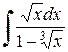

Решение.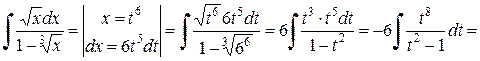

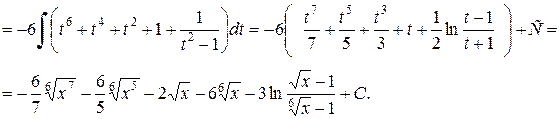
Замечание 2.5.1. Если подынтегральное выражение содержит функцию вида 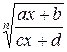, то следует использовать замену .

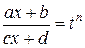2. а) Если подынтегральное выражение содержит простейшую квадратичную иррациональность вида 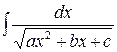, то путем выделения полного квадрата из квадратного трехчлена и замены переменной сводим интеграл к одному из двух следующих табличных интегралов: 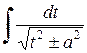или .

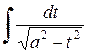Пример 2.5.2. Найти .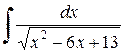

Решение.

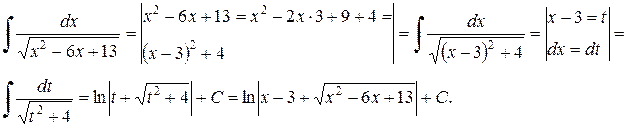
б) Если подынтегральное выражение содержит квадратичную иррациональность вида 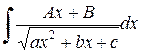, то путем выделения полного квадрата, замены переменной получаем сумму двух интегралов.

Пример 2.5.3. Найти .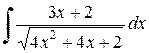

Решение.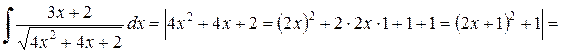

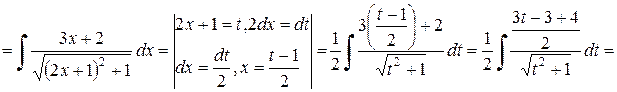
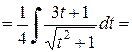
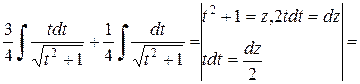
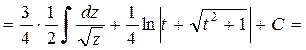
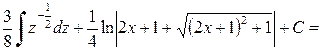
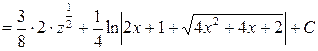
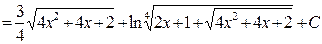
3. Если подынтегральное выражение содержит корень квадратный из квадратного трехчлена, т.е. 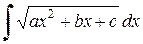. Решение производим в следующей последовательности: 1) выделим полный квадрат; 2) применим замену переменной; 3) к полученному выражению применяем метод интегрирования по частям.

Пример 2.5.4. Найти .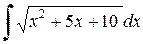

Решение.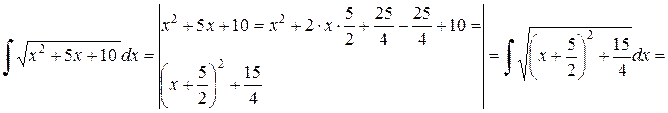

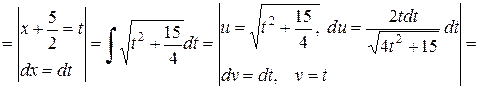
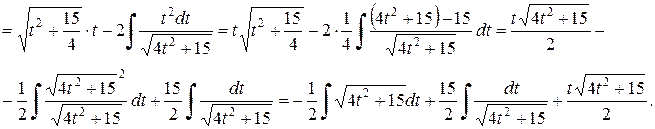
Таким образом, получим (запишем начало и конец):

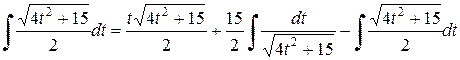
Приводим подобные члены полученного равенства:

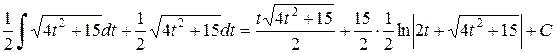
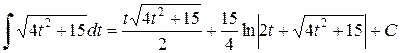
Возвращаясь с переменной 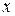, получим результат:

.

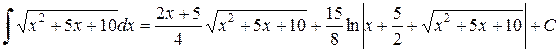4. а) Если подынтегральное выражение содержит корень квадратный из разности квадратов, т.е. 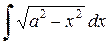. Решение производим используя замену 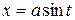(или ).

Пример 2.5.5. Найти .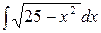

Решение.

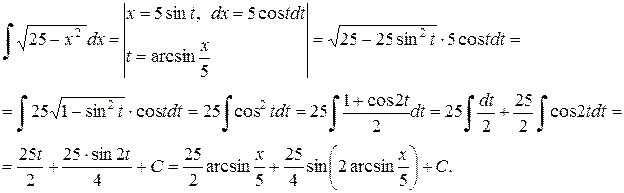
Полученный результат еще допускает упрощение, которое предлагается произвести самостоятельно.

б) Если подынтегральное выражение содержит корень квадратный из суммы квадратов, т.е. 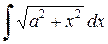. Решение можно производить используя замену 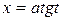или метод интегрирования по частям.

Замечание 2.5.2. При использовании метода интегрирования по частям результат достигается быстрее.

Предлагается решение примера 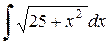произвести самостоятельно двумя способами, и сравнить: каким способом решение производится проще и быстрее.

5. Интегралы вида: 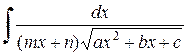решаются с помощью подста­новки .

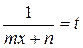Пример 2.5.6. Найти .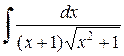

Решение. .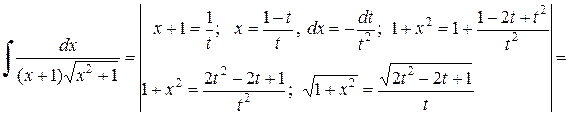

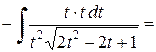
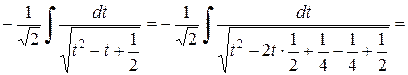
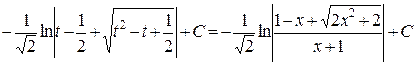6. Интегралы вида 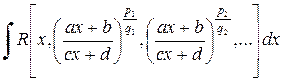,где 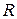- рациональная функция; 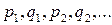- целые числа, находят с помощью замены 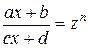, где - наименьшее общее кратное чисел .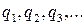

Пример 2.5.7. Найти .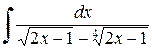

Решение. .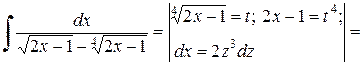

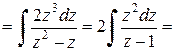
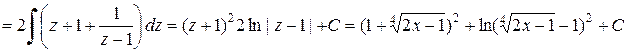Пример 2.5.8. Найти .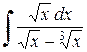

Решение.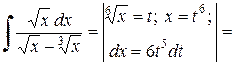

.

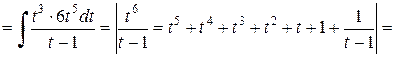
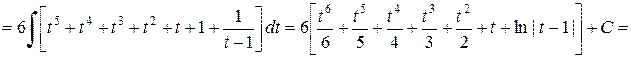
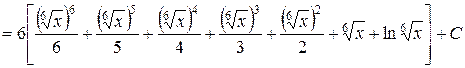7. Интегралы от дифференциальных биномов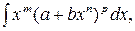

Дата добавления: 2015-10-30