
Читайте также:
|
Полагая 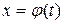 , где t – новая переменная и
, где t – новая переменная и  – непрерывная функция, дифференцируемая в области определения, будем иметь:
– непрерывная функция, дифференцируемая в области определения, будем иметь:
 . (2.1.1)
. (2.1.1)
Пример 2.1.1. Вычислить 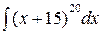 .
.
Решение.
 .
.
Пример 2.1.2. Найти  .
.
Решение.

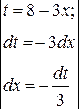
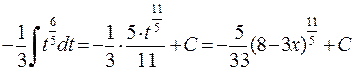 .
.
Пример 2.1.3. Найти  .
.
Решение.
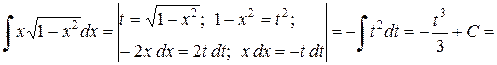
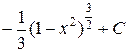 .
.
Интегрирование по частям
Формула интегрирования по частям: Если  и
и 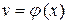 - дифференцируемые функции, то:
- дифференцируемые функции, то:
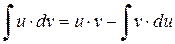 . (2.2.1)
. (2.2.1)
Умение разбить подынтегральное выражение на множители  и
и 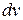 вырабатывается в процессе решения. Но можно указать основные типы интегралов, к которым применима формула интегрирования по частям.
вырабатывается в процессе решения. Но можно указать основные типы интегралов, к которым применима формула интегрирования по частям.
Если подынтегральное выражение имеет вид
1. 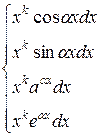
| рекомендуется обозначать: 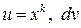 = = 
|
2. 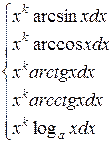
| рекомендуется обозначать  = = 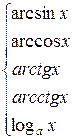
|
3. 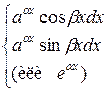
|  – любая из функций, но здесь обязательно требуется двукратное интегрирование по частям. – любая из функций, но здесь обязательно требуется двукратное интегрирование по частям.
|
Пример 2.2.1. Найти 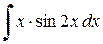 .
.
Решение.
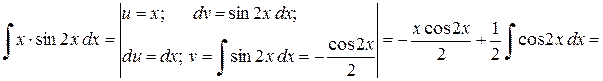
 .
.
Пример 2.2.2. Найти  .
.
Решение.
 .
.
Пример 2.2.3. Найти  .
.
Решение.
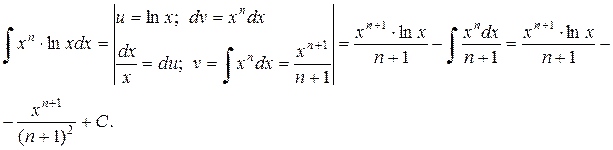 .
.
Пример 2.2.4. Найти 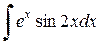 .
.
Решение.
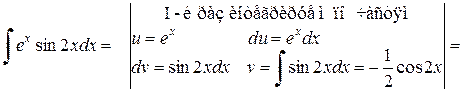

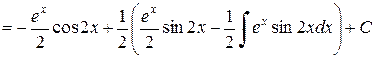 .
.
Приравняем начальное и конечное выражения:
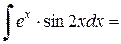
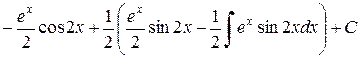
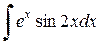
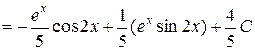 .
.
Интегрирование рациональных дробей
Рациональной дробью (функцией) называется дробь вида 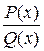 , где
, где 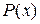 и
и  многочлены.
многочлены.
Рациональная дробь называется правильной, если степень многочлена 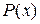 ниже степени многочлена
ниже степени многочлена  , в противном случае рациональная дробь называется неправильной.
, в противном случае рациональная дробь называется неправильной.
Если рациональная дробь неправильная, то путем почленного деления числителя на знаменатель по правилу деления многочленов (или с помощью алгебраических преобразований) следует выделить целую часть и неправильную рациональную дробь представить в виде суммы целой части и правильной рациональной дроби.
Поэтому будем рассматривать интегрирование правильных рациональных дробей, поскольку интегрирование целой части не вызывает затруднений.
Простые (правильные) рациональные дроби рассмотрим четырех типов:
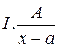 ,
, 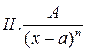 ;
; 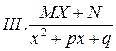 ;
;  ,
,
где 
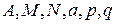 - действие числа; квадратный трехчлен
- действие числа; квадратный трехчлен 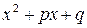 имеет отрицательный дискриминант, поэтому на множители не может быть разложен.
имеет отрицательный дискриминант, поэтому на множители не может быть разложен.
Рассмотрим интегрирование дробей каждого вида.
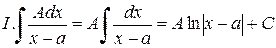 ;
;
 .
.
Пример 2.3.1. Найти 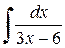 .
.
Решение.  .
.
Пример 2.3.2. Найти  .
.
Решение. 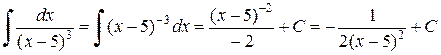 .
.
Пример 2.3.3. Найти 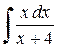 .
.
Решение.  .
.
Пример 2.3.4. Найти  .
.
Решение. 
 =
=  .
.
Дата добавления: 2015-10-30; просмотров: 115 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства неопределенного интеграла | | | Метода неопределенных коэффициентов |