
Читайте также:
|
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.
 (1.3.1)
(1.3.1)
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
 (1.3.2)
(1.3.2)
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
 (1.3.3)
(1.3.3)
где С – постоянного слагаемого.
4. Постоянный множитель можно выносить за знак интеграла, т.е.
 , (1.3.4)
, (1.3.4)
где  - некоторое число,
- некоторое число,  .
.
5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждой из этих функций:
 (1.3.5)
(1.3.5)
6. Если справедливо равенство: 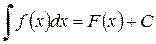 , то справедливым будет и соотношение:
, то справедливым будет и соотношение:
 . (1.3.6)
. (1.3.6)
Рассматривая функцию  как первообразную для некоторой функции
как первообразную для некоторой функции  , можно записать
, можно записать 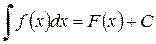 .
.
На основании свойства 2 и (1.3.2.) дифференциал неопределенного интеграла  , откуда
, откуда  .
.
Сравнивая между собой свойства 2 и 3, можно заключить, что операции нахождения неопределенного интеграла и дифференциала являються взаимообратными (знаки  и
и  взаимно уничтожают друг друга, в случае свойства 3 с точностью до постоянного слагаемого).
взаимно уничтожают друг друга, в случае свойства 3 с точностью до постоянного слагаемого).
Свойство 6 означает, что линейное изменение аргумента у функции под знаком интеграла ведет к аналогичному изменению аргумента первообразной, с поправкой на множитель  ).
).
Таблица основных интегралов и ее применение
| 1. | 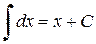 (1.4.1) (1.4.1)
|
| 2. | 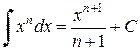 , ,  (1.4.2) (1.4.2)
|
| 3. |  (1.4.3) (1.4.3)
|
| 4. |  (1.4.4) (1.4.4)
|
| 5. |  (1.4.5) (1.4.5)
|
| 6. |  (1.4.6) (1.4.6)
|
| 7. | 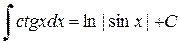 (1.4.7) (1.4.7)
|
| 8. |  (1.4.8) (1.4.8)
|
| 9. |  (1.4.9) (1.4.9)
|
| 10. |  (1.4.10) (1.4.10)
|
| 11. |  (1.4.11) (1.4.11)
|
| 12. |  (1.4.12) (1.4.12)
|
| 13. |  (1.4.13) (1.4.13)
|
| 14. | 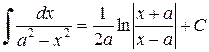 (1.4.14) (1.4.14)
|
| 15. |  (1.4.15) (1.4.15)
|
| 16. |  (1.4.16) (1.4.16)
|
| 17. |  (1.4.17) (1.4.17)
|
| 18. |  (1.4.18) (1.4.18)
|
Рассмотрим на примерах применение таблицы и некоторых свойств интегралов, (такие вычисления называются непосредственным интегрированием).
Пример 1.4.1. Найти  .
.
Решение. 
|  По свойству 5 для алгебраической суммы функций По свойству 5 для алгебраической суммы функций
|

| По табличным формулам (1.4.5), (1.4.3), (1.4.2), (1.4.13) возьмем интегралы и прибавим одну общую константу |
 . .
|
Пример 1.4.2. Найти  .
.
Решение.

| По формуле (1.4.13) при а = 5 получим |  . .
|
Пример 1.4.3. Найти 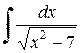 .
.
Решение.


 По формуле (1.4.18) при k = 7
По формуле (1.4.18) при k = 7  .
.
Пример 1.4.4. Найти  .
.
Решение.

Пример 1.4.5. Найти  .
.
Решение.

Пример 1.4.6. Найти  .
.

 Решение.
Решение.
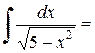 По формуле 17 при
По формуле 17 при  =
= 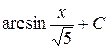 .
.
МЕТОДЫ ИНТЕГРИРОВАНИЯ
Дата добавления: 2015-10-30; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И | | | Интегрирование с помощью замены переменной |