Интегрирование тригонометрических функций

1. Интегралы вида можно вычислить, если их подынтегральные функции преобразовать по формулам:

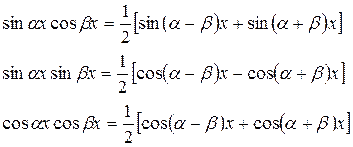(2.4.1.)

Пример 2.4.1. Найти .

Решение.

.

Пример 2.4.2. Найти .

Решение. .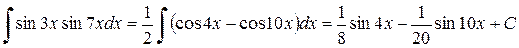

Пример 2.4.3. Найти

Решение. .

2. Случай четной степени одной функции.

Рассмотрим интеграл

а) 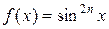, для понижения степени функции , используем формулу

б) , используем формулу

Пример 2.4.4. Найти

Решение.

.

Пример 2.4.5. Найти .

Решение.

.

3. Случай нечетной степени одной функции.

а) - отделением , функцию представляем в виде

и производим замену .

б) - поступаем аналогичным образом, т.е.

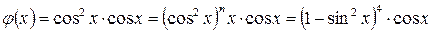, затем производим замену .

Пример 2.4.6. Найти .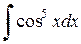

Решение. .

Пример 2.4.7. Найти .

Решение. =

.

4. Случай произведения двух функций вида:

а) оба показателя равные, т.е. , т.е. 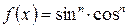- функцию переписываем в виде и, применив формулу , получим , а затем поступаем как в п.2., если - четное и как в п.3., если - нечетное.

б) показатели - четные, но . Решение проводим, как в п. 2.(а)

в) если один показатель четен, а другой нечетен, то решаем как в п. 3.

Пример 2.4.8. Вычислить .

Решение.

.

Пример 2.4.9. Найти .

Решение.

.

Пример 2.4.10. Найти .

Решение.

.

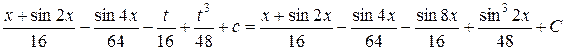Пример 2.4.11. Найти .

Решение.

.

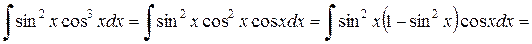
5. Случай произведения двух функций вида:

а) ;

б) (аргументы функций одинаковы).

Для нахождения интеграла используем замену той функции, которая возводится в степень.

Пример 2.4.12. Найти .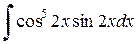

Решение.

Пример 2.4.13. Найти .

Решение.

.

6. Случай универсальной тригонометрической подстановки.

Универсальная подстановка 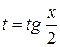применяется, когда под интегралом встречаются и с произвольными коэффициентами, при этом следует помнить выражения:

, , .

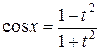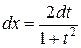После использования универсальной подстановки функция становится рациональной.

Пример 2.4.14. Найти .

Решение.

.

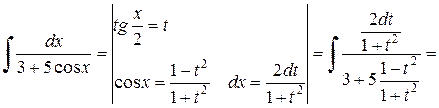
Замечание. Подстановка применяется, когда подынтегральная функция содержит 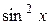, , с произвольными коэффициентами. В этом случае , , .

Пример 2.4.15. Найти .

Решение.

.

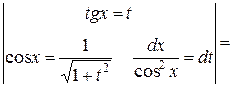
7. Тригонометрические подстановки

а) Если интеграл содержит радикал 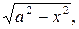то замена: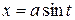

б) Если интеграл содержит радикал 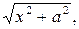то замена:

в) Если интеграл содержит радикал то замена:

Пример 2.4.16. Найти .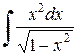

Решение.

.

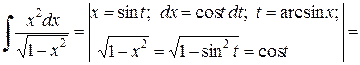
Пример 2.4.17. Найти .

Решение.

=

= .

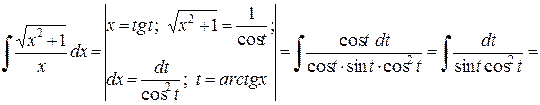
Пример 2.4.18. Найти .

Решение.

.

Дата добавления: 2015-10-30