
Читайте также:
|
ПРОИЗВОДНАЯ
1.1. Определение производной
Пусть на множестве 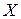 задана функция
задана функция  . Фиксируем точку
. Фиксируем точку 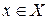 и задаем приращение аргумента
и задаем приращение аргумента 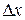 . Тогда точка
. Тогда точка  соответствует
соответствует  и
и  называется приращением функции.
называется приращением функции.
Если существует предел
 ,
,
то он называется производной функции  в точке
в точке 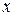 .
.
Существуют и другие обозначения производной: 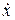 ,
,  .
.
Операция вычисления производной функции называется операцией дифференцирования, а если 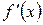 конечна, то функция
конечна, то функция  называется дифференцируемой.
называется дифференцируемой.
Прежде чем воспользоваться таблицами производных, надо установить, является функция простой или сложной.
Функция  называется сложной, если
называется сложной, если  есть функция от
есть функция от 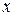 :
:  , т. е.
, т. е.  .
.
Производная сложной функции вычисляется по формуле
 ,
,
т. е. сначала вычисляется производная функции  по переменной
по переменной  , и затем она умножается на производную функции
, и затем она умножается на производную функции 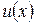 по переменной
по переменной 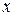 .
.
Правила дифференцирования
1.  (
( – const)
– const)
2. 
3. 
3а. 
4.  (
( )
)
5.  , если
, если  ,
,  .
.
Разумеется, что для справедливости этих правил необходимо существование производных  ,
, 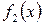 ,
,  ,
,  .
.
Таблица производных
1.  (
( ) 2.
) 2. 
3.  4.
4. 
5.  6.
6. 
7. 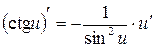 8.
8.  (
( )
)
9.  (
( ) 10.
) 10. 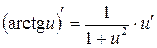
11.  12.
12.  (
( )
)
13.  14.
14. 
15. 
Пример 1. Найти производные функций:
а)  ; б)
; б) 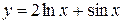 ; в)
; в)  .
.
Решение. а) Функция 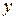 – это произведение двух функций
– это произведение двух функций  и
и  , поэтому по третьему правилу дифференцирования:
, поэтому по третьему правилу дифференцирования:
 .
.
Из таблицы производных находим, что 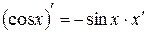 , и так как
, и так как  , то
, то 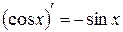 ;
;  .
.
Значит,  .
.
б) 
 .
.
в) 
 .
.
Пример 2. Найти производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
Решение. а) Функция 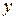 – это сложная функция
– это сложная функция 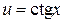 ,
,  . Тогда по формуле 1 таблицы производных
. Тогда по формуле 1 таблицы производных  , а по формуле 5
, а по формуле 5  .Таким образом,
.Таким образом,  .
.
б) Используем правило дифференцирования 3а:  . Функция
. Функция  – сложная
– сложная  ,
,  . Поэтому
. Поэтому
 .
.
в) 
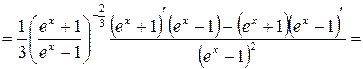
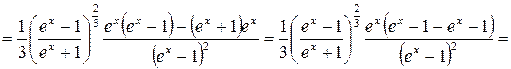
 .
.
Дифференцирование неявных функций
Если функция  такова, что подстановке ее в уравнение
такова, что подстановке ее в уравнение  , последнее обращается в тождество, то говорят о неявном задании функции
, последнее обращается в тождество, то говорят о неявном задании функции  . Например, уравнение
. Например, уравнение  неявно задает функцию
неявно задает функцию  (а также функцию
(а также функцию  ). Однако не всегда удается перейти от неявного задания функции к явному.
). Однако не всегда удается перейти от неявного задания функции к явному.
Пусть дифференцируемая функция  задана уравнением
задана уравнением  . Тогда дифференцируем левую и правую часть уравнения, считая
. Тогда дифференцируем левую и правую часть уравнения, считая 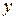 сложной функцией, и выражаем из уравнения
сложной функцией, и выражаем из уравнения  .
.
Пример 3. Найти производную функции  .
.
Решение.  ;
;  .
.
Так как  ,
,
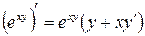 ,
,
 ,
,
 ,
,
то  .
.
Слагаемые, содержащие  , переносим в левую часть, а все остальное в правую:
, переносим в левую часть, а все остальное в правую:
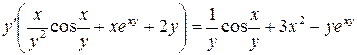 ,
,
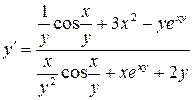 .
.
Дата добавления: 2015-10-23; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Перспективы разработки систем распознавания речи | | | Логарифмическое дифференцирование |