
Читайте также:
|
При вычислении предела отношения 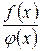 может оказаться, что при
может оказаться, что при 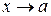 числитель и знаменатель одновременно стремятся к нулю или к бесконечности, то есть являются одновременно бесконечно малыми или бесконечно большими величинами. Говорят, что в этих случаях мы имеем дело с неопределенностями вида
числитель и знаменатель одновременно стремятся к нулю или к бесконечности, то есть являются одновременно бесконечно малыми или бесконечно большими величинами. Говорят, что в этих случаях мы имеем дело с неопределенностями вида 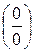 или
или 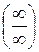 . Вычисление предела в этом случае называется «раскрытием неопределенности» и производится по правилу Лопиталя.
. Вычисление предела в этом случае называется «раскрытием неопределенности» и производится по правилу Лопиталя.
Правило Лопиталя. Пусть заданы две функции  и
и 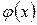 и выполняются условия:
и выполняются условия:
1) 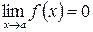 и
и 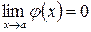 или
или
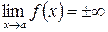 и
и 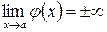 ;
;
2) они имеют первые производные в окрестности точки  (за возможным исключением самой точки
(за возможным исключением самой точки 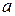 );
);
3) 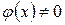 и
и 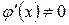 в окрестности точки
в окрестности точки 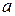 ;
;
4) существует 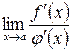 , тогда существует
, тогда существует 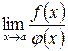 и имеет место равенство
и имеет место равенство 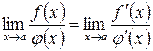 , если этот предел существует конечный или бесконечный.
, если этот предел существует конечный или бесконечный.
Сущность этого правила состоит в том, что в случае «неопределенностей» вида 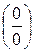 или
или 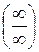 вычисление предела отношения функций, при соблюдении указанных требований, заменяется вычислением предела отношения их производных, которое в большинстве случаев оказывается проще.
вычисление предела отношения функций, при соблюдении указанных требований, заменяется вычислением предела отношения их производных, которое в большинстве случаев оказывается проще.
В случае, когда и отношение производных приводит в «неопределенностям» вида 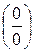 или
или 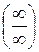 , снова применяют правило Лопиталя.
, снова применяют правило Лопиталя.
Пример 17. Найти 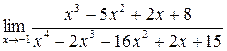 .
.
Решение. Если в данную дробь поставить 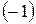 вместо
вместо 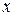 , то получится «неопределенность» вида
, то получится «неопределенность» вида 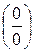 . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим:
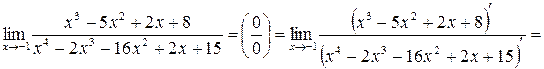
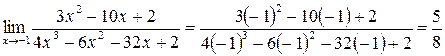 .
.
Пример 18. Найти 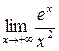 .
.
Решение. Здесь имеет место неопределенность 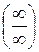 . Применяем правило Лопиталя:
. Применяем правило Лопиталя:
 .
.
В этом примере правило Лопиталя применили два раза.
Отметим, что правило Лопиталя применяется для раскрытия только «неопределенностей» вида 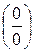 и
и 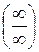 . Все остальные виды «неопределенностей» (
. Все остальные виды «неопределенностей» (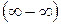 ,
, 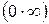 ,
, 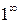 ,
, 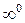 ,
, 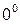 ) сначала приводятся к «неопределенностям»
) сначала приводятся к «неопределенностям» 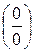 или
или 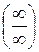 с помощью различных преобразований, а затем применяется правило Лопиталя.
с помощью различных преобразований, а затем применяется правило Лопиталя.
Раскрытие «неопределенности» 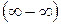 :
:
Если 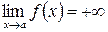 и
и 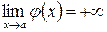 , то для определения предела
, то для определения предела 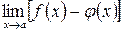 надо преобразовать разность
надо преобразовать разность 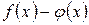 к виду
к виду
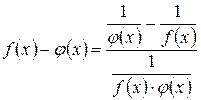 ,
,
тогда
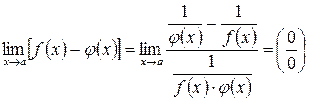
и раскрываем по правилу Лопиталя.
Пример 19. Найти 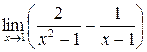 .
.
Решение. Если в данную дробь поставить 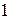 вместо
вместо 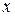 , то получится «неопределенность»
, то получится «неопределенность» 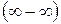 . Выражение, стоящее в скобках, приводим к общему знаменателю и получаем:
. Выражение, стоящее в скобках, приводим к общему знаменателю и получаем:
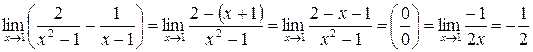 .
.
Раскрытие «неопределенности» 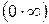 .
.
Пусть 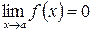 ,
, 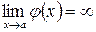 ;
;
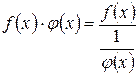 или
или 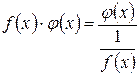 ,
,
тогда
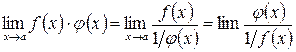 ,
,
то есть «неопределенность» вида 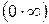 может быть сведена к «неопределенности» вида
может быть сведена к «неопределенности» вида 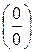 или
или 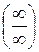 .
.
Пример 20. Найти 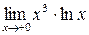 .
.
Решение. При 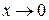
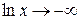 , а
, а 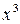 – величина бесконечно малая, поэтому здесь имеет место «неопределенность» вида
– величина бесконечно малая, поэтому здесь имеет место «неопределенность» вида 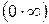 .
.
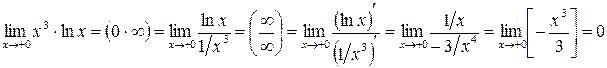 .
.
«Неопределенности» вида 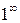 ;
; 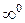 ;
; 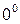 .
.
«Неопределенности» этих видов сводятся к «неопределенности» вида 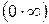 , которая была рассмотрена выше. Это достигается с помощью тождества.
, которая была рассмотрена выше. Это достигается с помощью тождества.
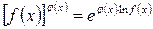 ; (
; (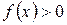 ),
),
тогда 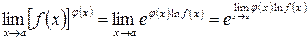 и все сводится к определению предела
и все сводится к определению предела 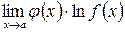 .
.
Пример 21. Найти  .
.
Решение. 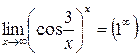 ;
; 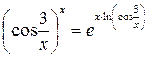 , поэтому
, поэтому
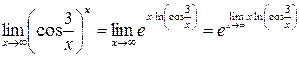 .
.
Найдем
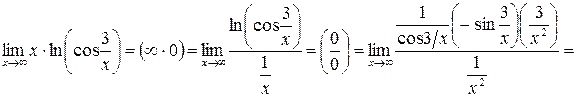
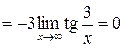 .
.
Окончательно получаем  .
.
Дата добавления: 2015-10-23; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ | | | Создание новой задачи |