Логарифмическое дифференцирование

Довольно часто возникает необходимость вычисления производной сложной функции 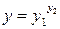, где , – дифференцируемые функции. В этом случае поступим следующим образом: логарифмируем –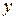

,

продифференцируем это равенство по –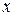

, .

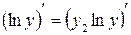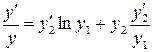Отсюда имеем:

.

Нет необходимости запоминать эту формулу. Достаточно понять идею – функцию сначала логарифмируем, затем дифференцируем полученное равенство и находим производную.

Пример 4. Найти производную функции .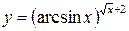

Решение. Логарифмируем функцию :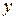

.

Дифференцируем это равенство по :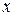

.

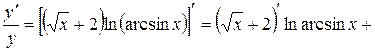
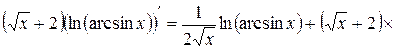
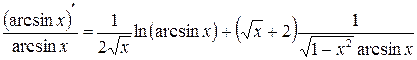Поэтому

.

Производные высших порядков

Если производная 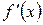функции определена в некоторой окрестности точки и имеет в этой точке производную, то эта производная от 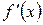называется второй производной (или производной второго порядка) функции в точке и обозначается одним из следующих символов:

, , , , , .

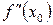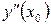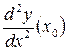Третья производная определяется как производная от второй производной и т. д. Если уже введено понятие -й производной и если -я производная имеет производную в точке , то указанная производная называется -й производной (или производной -го порядка) и обозначается

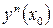, или , .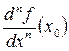

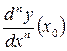Таким образом, производные высших порядков определяются индуктивно по формуле:

.

Функция, имеющая -ю производную в точке , называется раз дифференцируемой в этой точке.

Пример 5. Найти 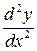функции .

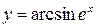Решение.

.

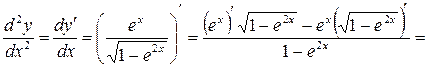
Пример 6. Найти 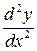, если .

Решение. Находим .

.

Теперь найдем вторую производную 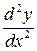. Имеем

.

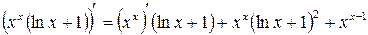Дифференцирование функции, заданной параметрически

Пусть даны две функции , (1)

где 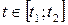назовем параметром. Причем имеет обратную функцию . Тогда из (1) 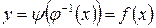, т. е. 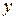является функцией от 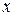. Задание функции через называется параметрическим.

Если функции , имеют производные и 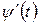, то функция также имеет производную, вычисляемую по формуле

. (2)

Вторая производная вычисляется по формуле

. (3)

Пример 7. Функция 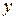задана параметрически: 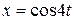, , 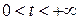. Найти и .

Решение. Найдем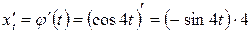

.

Тогда по формуле (2) .

Для вычисления найдем .

.

Подставим в формулу (3):

.

Дата добавления: 2015-10-23