Численное дифференцирование.

Данный раздел посвящен вопросам вычисление производных заданных порядков. Если аналитическое изображение исходной функции неизвестно или довольно сложное, производные любого порядка могут быть вычислены на основе приведенных в разделе формул дифференцирования. Большинство формул численного дифференцирования могут быть получены на основе интерполяционных полиномов. Для этого достаточно заменить начальную функцию ее интерполяционным полиномом, а потом вычислить производные от него. Если полином с достаточной точностью приближает исходную функцию, то можно утверждать, что производной любого порядка от полинома мало будут отличаться от производных функции.

В качестве примера применения численного дифференцирования приведем известный и широко применяющийся на практике пропорционально-интегрально-дифференциальный регулятор – ПИД-регулятор. Алгоритм его функционирования задается выражением

где P. I, D – числовые коэффициенты, устанавливаемые в процессе наладки для получения заданных показателей переходных процессов.

Особенностью технических систем является то, что зачастую мы не располагаем ни аналитическим описанием сигналов, ни даже таблицей значений входного сигнала.

Вспомним определение производной функции.

Из определения производной непосредственно следует простейшая формула для вычисления первой производной:

Эта формула может быть получена, если дифференцируемую функцию заменить отрезком прямой. Для вычислений используется текущее и предыдущее известное значение функции. Эта формула описывает так называемое дифференцирование «назад».

Очевидно, что если известна таблица значений функции, то можно определить производную функции, используя текущее и последующее значение – так называемое дифференцирование «вперед».

Приведем перечень практически применяющихся формул для численного дифференцирования таблично заданных функций.

Тип формулы	Формула
Несимметричные обратные, формулы дифференцирования «назад»
Несимметричные прямые, формулы дифференцирования «вперед»
Симметричные

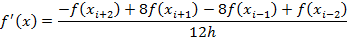
Симметричные формулы в общем случае имеют более высокую точность, однако они неприменимы для реализации алгоритмов, работающих в реальном времени.

Пример 9.2. Демонстрация простейших методов дифференцирования в программе MS Excel. В примере с помощью трех формул первого порядка рассчитывается производная функции y=sin(x).

Сравнительные графики производных, рассчитанных разными методами, приведены на рис. 9.5.

Рисунок 9.5 - Сравнительные графики производных синуса, рассчитанных разными методами.

Дата добавления: 2015-10-29