Метод половинного деления (метод дихотомии).

Считаем, что отделение корней уравнения (8.1) проведено и на отрезке [а,b] расположен один корень, который необходимо уточнить с допустимой погрешностью ε (рис. 8.1).

Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b]

х = (а+b)/2

и вычисляем функцию f(x). Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. На рис. 8.1 это будет отрезок [а, х₁] т.е. для очередного шага уточнения точку b перемещаем в середину отрезка х и продолжаем процесс деления как с первоначальным отрезком [а, b].

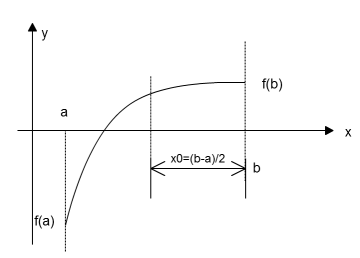
Рисунок 8.1 – Пояснение решению нелинейного уравнения методом половинного деления.

Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а, b] не станет меньше заданной погрешности ε.

Метод дихотомии позволяет значительно уменьшить объем вычислений
по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций интервал будет равен (b - а)/2ⁿ. За 10 итераций интервал уменьшится в 2¹⁰ = 1024, примерно в тысячу раз, за 20 итераций - в 2²⁰ примерно 10⁶ раз.

К недостаткам метода половинного деления относится относительно медленная сходимость. Кроме того, если корней на отрезке [а, b] несколько, то неизвестно, к какому корню сойдется процесс. Достоинством метода половинного деления есть простота и надежность.

Метод хорд.

Рассматриваемый метод так же, как и метод дихотомии, предназначен для уточнения корня на интервале [а, и], на концах которого левая часть решаемого уравнения f(x) принимает резные знаки.

Очередное приближение теперь в отличие от метода дихотомии берем не в середине отрезка, а в точке x_l где пересекает ось абсцисс прямая линия, проведенная через точки f(a) и f(b) (рис. 8.2).

Рисунок 8.2 – Пояснение к решению нелинейного уравнения методом хорд.

Уравнение прямой линии, проходящей через точки f₁= f(a) и f₂ = f(b), запишем в общем виде

у(х) = kх + с.

Коэффициенты к и с уравнения этой прямой определим из условий

f₁ = kа + с; f₂ = kb + с.

Вычитал левые и правые части последних соотношений, получим

Точку пересечения прямой у(х) с осью абсцисс получим, приравнивая у(х) нулю

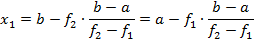
В зависимости от знака функции в уточненной точке x₁ на основании теоремы Больцано-Коши уточняем, какой отрезок будет использован для следующего шага поиска.

Процесс поиска корня останавливается тогда, когда расстояние между очередными приближениями станет меньше заданной погрешности ε:

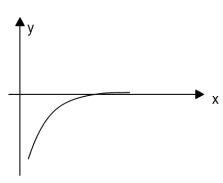
Дискуссионный вопрос. Предположим, что график заданной функции хотя и имеет единственный корень, но имеет особенность: он очень медленно изменяется в районе нуля. Какие проблемы возникнут при использовании метода секущих или метода половинного деления, при отыскании корня подобной функции?

Дата добавления: 2015-10-29