Итерационные методы.

Для получения гарантированной точности получаемого решения, а также для решения СЛАУ высоких (несколько тысяч) размерностей следует применять итерационные методы решения СЛАУ.

Итерационные методы относятся к классу методов последовательного приближения.

Идея итерационных методов решения СЛАУ состоит в следующем.

Запишем уравнения исходной СЛАУ в виде

Задается столбец начальных приближений , подставляя эти значения в правые части приведенной выше системы уравнений получим новое приближение решения . Повторяя этот вычислительный процесс достаточное число раз, мы получаем на каждом шаге все более точное значение решений СЛАУ.

При использовании итерационных вычислительных процессов любого вида необходимо учитывать некоторые особенности:

1. Итерационный процесс может быть расходящимся. Устойчивость вычислительного процесса часто зависит от значений начального приближения, выбранного для старта процесса. Необходимо контролировать устойчивость и сходимость итерационного процесса.

2. Сходящийся итерационный процесс не обязательно сходится к точному решению исходной системы. Поэтому необходимо обязательно проверять полученные решения путем прямой подстановки полученных решений в исходную СЛАУ.

Описанная выше вычислительная схема носит название метода простых итераций.

Для повышения сходимости и точности итерационного процесса можно предложить следующий несложный подход. При вычислении каждого итерационного уравнения вместо значений переменных на предыдущем шаге расчетов можно использовать уточненные значения переменных, полученные из уже преобразованных уравнений текущего шага расчетов:

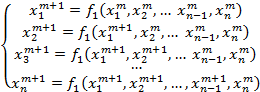
Такое изменение итерационного процесса, известное как метод Зейделя, как правило приводит к ускорению сходимости.

Для сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами. Условие сходимости можно обеспечить преобразованием исходной матрицы путем перестановки уравнений и неизвестных. Методы простых итераций Зейделя имеют разные области сходимости. Эти методы можно применять и к решению систем нелинейных уравнений.

Заканчиваем итерационный процесс, когда выполнятся условия

где ε - заданная погрешность; k = 1,2,… n.

Если условие завершения итерационного процесса не выполняется, то этот процесс может выполняться неограниченно долго. При реализации итерационных вычислительных схем обязательно предусматривается максимально возможное число итераций, при превышении которого вычисления заканчиваются независимо от достигнутой точности.

В общем случае, итерационные процедуры решения СЛАУ выполняются гораздо быстрее прямых методов СЛАУ. Их недостатком является то, что решение СЛАУ находится с ограниченной точностью, а итерационный вычислительный процесс может быть расходящимся.

Дата добавления: 2015-10-29