Степенной базис

Выберем базисные функции φ_k(х) в виде последовательности степеней аргумента х, которые линейно независимы,

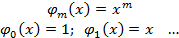(5.4)

В этом случае так же, как и при интерполяции, мы будем аппроксимировать экспериментальную зависимость полиномом. Однако степень полинома n выбираем обычно m<<n (при лагранжевой интерполяции m=n).

Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Экспериментальные данные "сглаживаются" с помощью функции φ(х). Если же выбрать m = n, то на основании единственности интерполяционного полинома получим функцию φ(х), совпадающую с каноническим интерполяционным полиномом степени n, аппроксимирующая кривая пройдет через все экспериментальные точки и величина Q будет равна нулю. Последнее обстоятельство используется для отладки и тестирования программ, реализующих алгоритмы МНК.

Запишем расширенную матрицу системы нормальных уравнений для базиса (5.4):

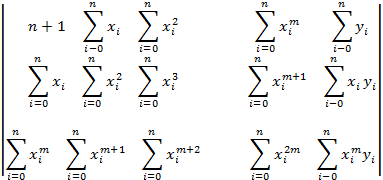
Нетрудно видеть, что для формирования расширенной матрицы (5.5)достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы не являются "оригинальными" и заполняются с помощью циклического присвоения.

Пример 5.1. Рассмотрим линейную аппроксимацию экспериментальных данных, т.е. аппроксимацию в виде прямой y = ax + b. В этом случае m = 1

Запишем расширенную матрицу Грама для этого случая:

Тогда, используя метод Крамера, получим следующие расчетные формулы для коэффициентов аппроксимирующей прямой:

Пример 5.2. Аппроксимация функций в MATLAB.

x = [1 2 3 4 5];

y = [4 2 0 1 -2];

% Построим интерполяционный многочлен (аппроксимация первой степени)

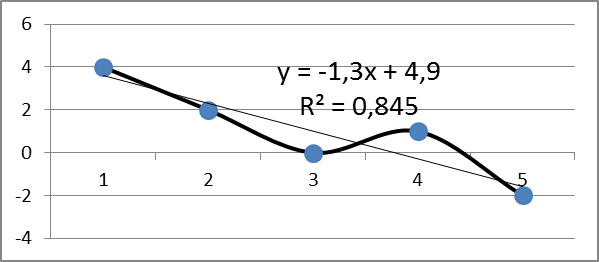
p = polyfit(x, y, 1)

p =

-1.3000 4.9000

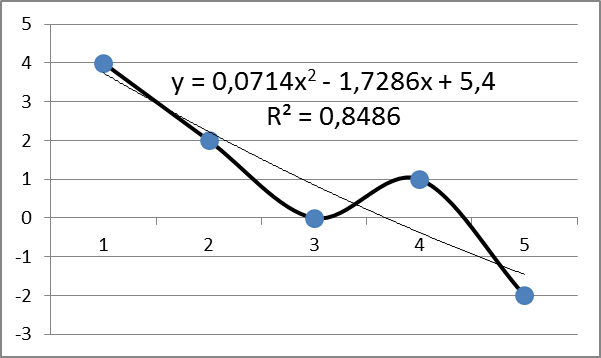
При аппроксимации полиномом второй степени получим

p =

0.0714 -1.7286 5.4000

Пример 5.2. Аппроксимация функций в Excel.

Исходные данные в таблице:

x	y
	-2

Вычисленное уравнение линейной регрессии размещается на графике:

Дата добавления: 2015-10-29