
|
Читайте также: |
Любой элемент линейного пространства V /К можно записать в виде линейной комбинации элементов базиса 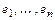 и притом единственным образом:
и притом единственным образом:
 .
.
Коэффициенты  называются координатами вектора
называются координатами вектора  .
.
Свойства координат:
1) Два вектора равны  их координаты равны.
их координаты равны.
2) Для того, чтобы сложить два вектора, надо сложить их координаты.
3) Для того, чтобы умножить вектор на элемент 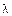 поля, надо умножить на
поля, надо умножить на 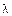 каждую координату вектора.
каждую координату вектора.
Пусть в линейном пространстве V /K даны два базиса: 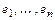 и
и 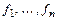 . Разложим элементы второго базиса по первому базису:
. Разложим элементы второго базиса по первому базису:

Если ввести обозначения
 ,
,
то эту систему равенств можно переписать в матричном виде:
 .
.
Матрица А называется матрицей перехода от базиса е к базису f. Матрица А невырождена, так как векторы 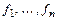 линейно независимы, поэтому существует матрица
линейно независимы, поэтому существует матрица  и
и
 .
.
Пусть  координаты вектора
координаты вектора  в базисе
в базисе 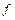 . Тогда
. Тогда 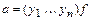 . Вместе с равенствами
. Вместе с равенствами 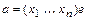 и
и  это дает условие
это дает условие  . Отсюда, координаты
. Отсюда, координаты  вектора
вектора  в базисе
в базисе 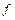 связаны с координатами
связаны с координатами 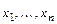 в базисе
в базисе  формулами перехода:
формулами перехода:

Пример. Показать, что векторы 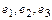 сами образуют базис и найти координаты вектора
сами образуют базис и найти координаты вектора  в этом базисе:
в этом базисе:
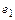 =(1,1,1),
=(1,1,1),  =(1,1,2),
=(1,1,2), 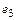 =(1,2,3);
=(1,2,3);  =(6,9,14).
=(6,9,14).
Найдем ранг матрицы, составленной из координат векторов 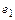 ,
,  и
и 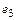 :
:

Ранг равен трем, следовательно, векторы линейно независимы, а любые три линейно независимых вектора в трехмерном пространстве образуют базис.
Пусть  . Тогда
. Тогда

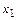 (1,1,1)+
(1,1,1)+  (1,1,2)+
(1,1,2)+  (1,2,3)=
(1,2,3)=
 (6,9,14),
(6,9,14),

Координаты вектора  в новом базисе (1,2,3).
в новом базисе (1,2,3).
Пример. Даны два базиса линейного пространства столбцов:
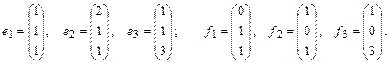
Найти:
а) матрицу А перехода от базиса 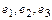 к базису
к базису  ;
;
б) матрицу  обратного перехода;
обратного перехода;
в) координаты 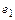 в обоих базисах;
в обоих базисах;
г) координаты вектора  в базисе
в базисе 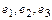 , имеющего во втором базисе координаты (5 3 1).
, имеющего во втором базисе координаты (5 3 1).

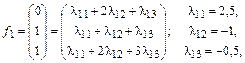


а)  б)
б) 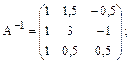
в) 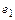 имеет координаты (1,0,0) в первом базисе и координаты (2,5,-1,-0,5) во втором;
имеет координаты (1,0,0) в первом базисе и координаты (2,5,-1,-0,5) во втором;
г) координаты вектора  в базисе
в базисе 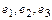 вычисляем по формуле:
вычисляем по формуле:

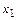 =5,5,
=5,5,  =-1,
=-1,  =0,5.
=0,5.
Упражнения
1) Как изменится матрица перехода от одного базиса к другому, если:
а) поменять местами два вектора первого базиса?
б) поменять местами два вектора второго базиса?
2) Найти координаты вектора  в базисе
в базисе 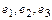 , если
, если 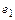 =(1, 1, 1, 1),
=(1, 1, 1, 1),  = (1, 1, -1, -1),
= (1, 1, -1, -1), 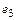 = (1, -1, 1, -1),
= (1, -1, 1, -1),  = (1, -1, -1, -1),
= (1, -1, -1, -1),  = (1, 2, 1, 1).
= (1, 2, 1, 1).
3) Найти формулы преобразования координат при переходе от базиса  к базису
к базису  , если
, если
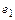 =(1, 2, -1, 0),
=(1, 2, -1, 0),  = (2, 1, 0,1),
= (2, 1, 0,1),
 = (1, -1, 1, 1),
= (1, -1, 1, 1),  = (0, 1, 2, 2),
= (0, 1, 2, 2),
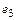 = (-1, 2, 1, 1),
= (-1, 2, 1, 1),  = (-2, 1, 1,2),
= (-2, 1, 1,2),
 = (-1, -1, 0, 1);
= (-1, -1, 0, 1); 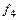 = (1, 3, 1, 2).
= (1, 3, 1, 2).
4) Уравнение поверхности относительно базиса  имеет вид
имеет вид  . Найти уравнение этой поверхности относительно базиса
. Найти уравнение этой поверхности относительно базиса  = (1, 1, 1,1),
= (1, 1, 1,1),  = (1, 1, -1, -1),
= (1, 1, -1, -1),  = (1, -1, 1,-1),
= (1, -1, 1,-1), 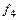 = (1, -1, -1, 1).
= (1, -1, -1, 1).
Дата добавления: 2015-10-23; просмотров: 1666 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Эквивалентные системы. Базис и размерность | | | Изоморфизм линейных пространств |