
Читайте также:
|
МАТРИЦЫ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Учебно-методическое пособие
Томск
РАССМОТРЕНО и УТВЕРЖДЕНО методической комиссией факультета прикладной математики и кибернетики.
ПРОТОКОЛ № 26 от 26 января 2007 г.
Председатель комиссии
профессор С.Э.Воробейчиков
В учебно-методическом пособии приведены краткие теоретические сведения и даны практические рекомендации к решению задач по курсу «Линейная алгебра и аналитическая геометрия».
Пособие разработано для студентов факультета прикладной математики и кибернетики дневной формы обучения.
Составители: К.И.Лившиц
Л.Ю.Сухотина

1. Матрицы
Основные понятия
Определение. Пусть  — множество чисел и
— множество чисел и 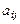 — набор из
— набор из  элементов множества
элементов множества  . Прямоугольная таблица
. Прямоугольная таблица
 ,
,
состоящая из 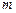 строк и
строк и  столбцов, называется матрицей.
столбцов, называется матрицей.
Числа 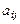 , входящие в состав данной матрицы, называются ее элементами. Совокупность элементов
, входящие в состав данной матрицы, называются ее элементами. Совокупность элементов 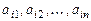 образуют
образуют  ю строку матрицы, а совокупность элементов
ю строку матрицы, а совокупность элементов  образует
образует  й столбец матрицы. Величины
й столбец матрицы. Величины 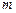 и
и  называются порядками матрицы.
называются порядками матрицы.
Две матрицы, имеющие одинаковое число 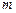 строк и одинаковое число
строк и одинаковое число  столбцов называются матрицами одинакового типа. Две матрицы
столбцов называются матрицами одинакового типа. Две матрицы  и
и  называются равными, если они имеют одинаковые порядки и
называются равными, если они имеют одинаковые порядки и  .
.
Если  , матрица называется квадратной. Совокупность элементов
, матрица называется квадратной. Совокупность элементов  называется главной диагональю матрицы. Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной. Если все диагональные элементы диагональной матрицы
называется главной диагональю матрицы. Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной. Если все диагональные элементы диагональной матрицы 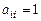 , то диагональная матрица называется единичной и обозначается символом
, то диагональная матрица называется единичной и обозначается символом  .
.
Матрица, у которой все элементы равны нулю, называется нулевой матрицей и обозначается  . Нулевые матрицы различных порядков считаются различными, так как состоят из разного числа элементов.
. Нулевые матрицы различных порядков считаются различными, так как состоят из разного числа элементов.
Квадратная матрица называется верхней треугольной, если из  следует, что
следует, что  и нижней треугольной, если из
и нижней треугольной, если из  следует, что
следует, что  .
.
Матрицу, состоящую из одной строки, называют вектор — строкой, а матрицу, состоящую из одного столбца, называют вектор — столбцом. Например, матрица  вектор — строка размера
вектор — строка размера 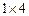 .
.
Действия с матрицами
1. Транспонирование матриц. Операция транспонирования матриц состоит в перемене местами строк и столбцов с сохранением их номеров. Пусть дана матрица  порядка
порядка  . Тогда транспонированной по отношению матрице
. Тогда транспонированной по отношению матрице  называется матрица
называется матрица  порядка
порядка  , элементы которой
, элементы которой 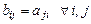 . Транспонирование матрицы обозначается как
. Транспонирование матрицы обозначается как  .
.
Пример. Пусть  Тогда
Тогда 
2. Сложение матриц. Операция сложения вводится только для матриц одинакового типа. Суммой двух матриц  и
и  одинакового типа называется матрица
одинакового типа называется матрица  того же типа, элементы которой
того же типа, элементы которой 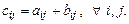 Используется обозначение
Используется обозначение 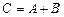 .
.
3. Умножение матрицы на число. Произведением матрицы  порядка
порядка  и числа
и числа  называется матрица
называется матрица  того же типа, элементы которой
того же типа, элементы которой  . Используется обозначение
. Используется обозначение  .
.
Пример. Пусть 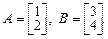
Тогда матрица 
4. Умножение матрицы на матрицу. Операция умножения матрицы  на матрицу
на матрицу  вводится для прямоугольных матриц при условии, что число столбцов матрицы
вводится для прямоугольных матриц при условии, что число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 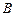 . Произведением матрицы
. Произведением матрицы  порядка
порядка 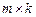 и матрицы
и матрицы 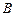 порядка
порядка  , заданных в определенном порядке (
, заданных в определенном порядке ( — первая,
— первая, 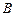 — вторая), называется матрица
— вторая), называется матрица  порядка
порядка  , элементы которой
, элементы которой
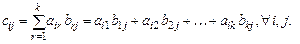
Таким образом, элемент  матрицы
матрицы  есть сумма произведений элементов
есть сумма произведений элементов  - й строки матрицы
- й строки матрицы  на соответствующие элементы
на соответствующие элементы  - го столбца матрицы
- го столбца матрицы 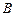 .
.
Пример 1. Пусть  . Тогда
. Тогда
 ,
,
 .
.
Пример 2. Пусть  . Тогда
. Тогда
 .
.
Задачи
Вычислить произведения матриц:
1.  2.
2.  . 3.
. 3.  .
.
4. 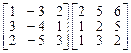 . 5.
. 5.  .
.
6. Доказать, что если для матриц  и
и 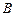 оба произведения
оба произведения  и
и 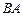 существуют, причем
существуют, причем 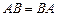 , то матрицы
, то матрицы  и
и 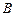 - квадратные и имеют одинаковый порядок.
- квадратные и имеют одинаковый порядок.
Вычислить выражения:
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  , порядок матрицы равен
, порядок матрицы равен  .
.
11. Найти значение многочлена  от матрицы
от матрицы  .
.
12. Доказать, что если матрицы  и
и 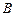 - квадратные и имеют одинаковый порядок, причем
- квадратные и имеют одинаковый порядок, причем  , то
, то
а)  . б)
. б)  .
.
13. Доказать, что если матрицы  и
и 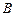 - квадратные и имеют одинаковый порядок, причем
- квадратные и имеют одинаковый порядок, причем 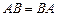 , то
, то
 .
.
14. Найти все матрицы, перестановочные с матрицей
 .
.
Определители
Основные понятия
Понятие определителя вводится только для квадратных матриц. Пусть  — квадратная матрица порядка
— квадратная матрица порядка  . Составим произведение из
. Составим произведение из  различных элементов матрицы
различных элементов матрицы  , выбирая по одному и только одному элементу из каждой строки и каждого столбца. Запишем это произведение в виде
, выбирая по одному и только одному элементу из каждой строки и каждого столбца. Запишем это произведение в виде  . Будем называть его членом определителя. Рассмотрим последовательность чисел
. Будем называть его членом определителя. Рассмотрим последовательность чисел  . По самому построению члена определителя это различные числа, которые представляют собой перестановку чисел от 1 до
. По самому построению члена определителя это различные числа, которые представляют собой перестановку чисел от 1 до  . Назовем инверсией в перестановке
. Назовем инверсией в перестановке  такое расположение чисел, когда старшее стоит перед младшим. Например, в перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий. Обозначим число инверсий в перестановке через
такое расположение чисел, когда старшее стоит перед младшим. Например, в перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий. Обозначим число инверсий в перестановке через 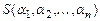 . Так как из
. Так как из  чисел можно составить
чисел можно составить  различных перестановок, то число различных членов определителя равно
различных перестановок, то число различных членов определителя равно  !
!
Определение. Определителем (детерминантом) матрицы  называется алгебраическая сумма
называется алгебраическая сумма  ! членов определителя перед каждым из которых стоит знак
! членов определителя перед каждым из которых стоит знак  . Или
. Или

где сумма берется по всем возможным перестановкам  .
.
Хотя определитель матрицы это число, будем для удобства столбцы и строки матрицы  называть также столбцами и строками ее определителя
называть также столбцами и строками ее определителя  .
.
Пример. Вычислим определитель матрицы второго порядка
 .
.
Члены определителя имеют вид  , где
, где 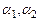 принимают значения 1 и 2. Возможны две пары значений
принимают значения 1 и 2. Возможны две пары значений  и
и  . Поэтому
. Поэтому
 .
.
Дата добавления: 2015-10-26; просмотров: 172 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Примечание к части | | | Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке |