Обратная матрица

Квадратная матрица называется обратной по отношению к квадратной матрице того же порядка, если

.

Необходимым и достаточным условием существования обратной матрицы является невырожденность матрицы т.е.

.

В этом случае обратная матрица существует, является единственной и определяется соотношением

,

где алгебраические дополнения элементов матрицы .

Обратная матрица обладает следующими свойствами:

1. .

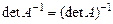2. .

3. .

Полезно помнить, что если матрица является треугольной, то является треугольной того же типа, что и матрица . Обратная к симметричной матрице тоже симметрична.

Пример. Найти матрицу обратную к матрице

.

Определитель 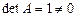и, следовательно, обратная матрица существует. Алгебраические дополнения элементов матрицы равны

Поэтому

.

Задачи

Найти матрицы обратные к данным.

1. . 2. . 3. .

4. . 5. .

6. .

7. Решить матричные уравнения:

а) .

б) .

8. Показать, что вычисление матрицы, обратной к данной матрице порядка , можно свести к решению систем линейных уравнений, каждая из которых содержит уравнений с неизвестными и имеет матрицей коэффициентов при неизвестных матрицу .

9. Как изменится обратная матрица , если в данной матрице :

а) переставить ю и ю строки?

б) ю строку умножить на число ?

в) к й строке прибавить ю, умноженную на число , или совершить аналогичное преобразование столбцов?

Ранг матрицы

Основные понятия

Определение 1. Пусть даны 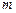вектор – столбцов порядка

и 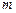скаляров . Умножая на и складывая, получим вектор – столбец с элементами , который называется линейной комбинацией столбцов .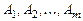

Определение 2. Столбцы 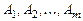называются линейно зависимыми, если найдутся такие числа , не равные нулю одновременно, что линейная комбинация

,

где ноль справа это нулевой вектор – столбец.

Определение 3. Столбцы 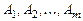называются линейно независимыми, если равенство

возможно только при условии .

Необходимым и достаточным условием линейной зависимости вектор – столбцов является равенство одного из них линейной комбинации других.

Пример. Пусть даны вектор – столбцы

.

Нетрудно заметить, что столбец равен сумме . Поэтому при 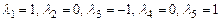линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.

В общем случае проверка условия линейной зависимости сводится к нахождению ненулевого решения системы уравнений

Рассмотрим теперь матрицу порядка .

Определение 4. Натуральное число называется рангом матрицы , если у нее имеется минор порядка отличный от нуля, а все миноры порядка 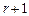и выше, если это возможно, равны нулю. Очевидно, что .

Определение 5. Если ранг матрицы равен , то всякий отличный от нуля минор порядка матрицы называется базисным минором. Строки и столбцы матрицы , на пересечении которых расположен базисный минор, называются базисными строками и столбцами.

Теорема (о базисном миноре). Базисные столбцы (строки) матрицы линейно независимы. Любой столбец (любая строка) матрицы является линейной комбинацией базисных столбцов (строк).

Из последних утверждений следует второе определение ранга матрицы: ранг матрицы равен максимальному числу ее линейно независимых столбцов (строк).

Дата добавления: 2015-10-26