
Читайте также:
|
Основным приемом вычисления определителя  го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
Пример 1. Вычислить определитель

Разложим определитель по первому столбцу. Получим
 .
.
Таким образом, вычисление определителя четвертого порядка свелось к вычислению четырех определителей третьего порядка. Далее, разлагая определители третьего порядка по первому столбцу, получим
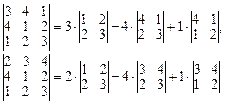
и т.д. Окончательно получим  .
.
Вычисления значительно упростятся, если воспользоваться свойствами определителя. По свойству 7 можно, не меняя значения определителя, прибавить второй, третий и четвертый столбцы к первому, а затем первую строку вычесть из второй, третьей и четвертой. Получим

Пример 2. Вычислить определитель треугольной матрицы  го порядка
го порядка
 .
.
Для вычисления разложим определитель по последней строке. Получим, что  , где
, где  треугольный определитель порядка
треугольный определитель порядка  . Определитель
. Определитель  снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что
снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что  .
.
Пример 3. Вычислить определитель матрицы  го порядка
го порядка
 .
.
Подобные определители можно достаточно просто преобразовать к треугольному виду. Для этого прибавим все столбцы к первому и затем вычтем первую строку из всех остальных. Получим

Пример 4. Следующий метод вычисления определителей  го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
Рассмотрим идею метода на примере вычисления определителя трехдиагональной матрицы или матрицы Якоби (матрицей Якоби называется матрица  , если из
, если из 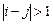 следует
следует  ). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
 ,
,
где  и
и  постоянные числа. Для нахождения
постоянные числа. Для нахождения  необходимо решить полученное уравнение. Заменим
необходимо решить полученное уравнение. Заменим  соответствующей степенью переменной
соответствующей степенью переменной 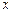
 .
.
Перенося все слагаемые в левую часть и сокращая на 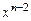 , получим квадратное уравнение
, получим квадратное уравнение  , называемое характеристическим уравнением. Пусть
, называемое характеристическим уравнением. Пусть  корни этого уравнения. Тогда возможны два случая:
корни этого уравнения. Тогда возможны два случая: 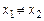 и
и  .
.
Если 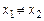 , то определитель
, то определитель  имеет вид
имеет вид
 ,
,
где числа  находятся из условий
находятся из условий
 .
.
Определители  и
и  в левых частях условий вычисляются непосредственно из вида
в левых частях условий вычисляются непосредственно из вида  .
.
Если  , то
, то
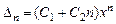 ,
,
а числа  находятся из условий
находятся из условий
 .
.
Рассмотрим конкретный пример. Вычислим определитель  го порядка
го порядка
 ,
,  .
.
Разложим определитель по последнему столбцу
 .
.
Первый определитель в правой части является определителем порядка  того же типа, что и
того же типа, что и  . Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и
. Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и  , но порядка
, но порядка  . В итоге получим рекуррентное соотношение для
. В итоге получим рекуррентное соотношение для 
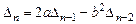 .
.
Соответствующее характеристическое уравнение

имеет корни  и
и  . Так как
. Так как  , то
, то 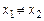 и
и  . Из вида
. Из вида  находим
находим
 .
.
Тогда для определения  получим систему уравнений
получим систему уравнений


решая которую, находим

(при решении использовались равенства:  ). Тогда
). Тогда
 .
.
Пример 5. Вычислить определитель  го порядка
го порядка
 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых:  . Тогда по свойству 3. определитель представится в виде суммы двух определителей
. Тогда по свойству 3. определитель представится в виде суммы двух определителей
 .
.
Первый определитель разложим по последнему столбцу. Второй определитель приведем к треугольному виду, вычитая последний столбец из всех остальных. Тогда
 (1)
(1)
где  является определителем порядка
является определителем порядка  того же типа, что и
того же типа, что и  .
.
Решим полученное уравнение для  . Из вида
. Из вида  при
при  имеем
имеем  .Выписывая (1) при
.Выписывая (1) при  с учетом равенства для
с учетом равенства для  , получаем
, получаем
 .
.
Методом математической индукции теперь нетрудно показать, что  .
.
Пример 6. Вычислить определитель  го порядка
го порядка
 .
.
Представим элементы последнего столбца в виде суммы двух слагаемых:  и распишем определитель как сумму двух определителей
и распишем определитель как сумму двух определителей
 .
.
Первый определитель разложим по последнему столбцу. Для вычисления второго определителя умножим последний столбец на 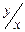 и вычтем из остальных. Получим
и вычтем из остальных. Получим

Для решения полученного рекуррентного соотношения воспользуемся тем, что при транспонировании матрицы ее определитель не меняется. В нашем случае транспонировании приводит к замене 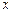 на
на  наоборот. Поэтому имеем два равенства
наоборот. Поэтому имеем два равенства

Откуда  .
.
Пример 7. Следующий пример иллюстрирует применение теоремы Лапласа. Нужно вычислить определитель квазитреугольной матрицы порядка  . Квазитреугольной называют блочную матрицу вида
. Квазитреугольной называют блочную матрицу вида  , где
, где 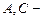 квадратные матрицы,
квадратные матрицы,  прямоугольная матрица,
прямоугольная матрица,  нулевая матрица. В подробной записи матрица имеет вид
нулевая матрица. В подробной записи матрица имеет вид
 .
.
Пусть  . Покажем, что
. Покажем, что  . Воспользуемся теоремой Лапласа. Разложим этот определитель по первым
. Воспользуемся теоремой Лапласа. Разложим этот определитель по первым  строкам. Очевидно, что из первых
строкам. Очевидно, что из первых  строк можно составить только один минор
строк можно составить только один минор  го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию
го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию  . Этот минор есть
. Этот минор есть  . Дополнительным к нему минором является определитель
. Дополнительным к нему минором является определитель  , что и доказывает формулу.
, что и доказывает формулу.
Задачи
1. Определить число инверсий в перестановках:
а) 1,9.6,3.2.4.7.8.
б)  .
.
в)  .
.
2. Выбрать значения  и
и  так, чтобы произведение
так, чтобы произведение  входило в определитель 7-го порядка со знаком плюс.
входило в определитель 7-го порядка со знаком плюс.
3. С каким знаком входит в определитель порядка  произведение элементов побочной диагонали?
произведение элементов побочной диагонали?
4. Найти члены определителя
 ,
,
содержащие  и
и  .
.
5. Пользуясь только определением, вычислить определитель
 .
.
6. Пользуясь только свойствами определителей вычислить следующие определители:
а)  . б)
. б)  .
.
в)  . г)
. г)  .
.
д)  , где
, где  .
.
7. Не вычисляя определителей, доказать следующие тождества:
а)  .
.
б)  .
.
в)  .
.
г)  .
.
8. Пользуясь свойствами определителей, включая разложение по строке или столбцу, доказать тождество:
 .
.
9. Разлагая по 2-му столбцу, вычислить определитель
 .
.
Вычислить определители:
10.  . 11.
. 11.  . 12.
. 12.  .
.
13. 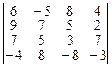 . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
В следующих задачах, где по виду определителя нельзя установить его порядок, предполагается, что он равен  .
.
Вычислить следующие определители, приводя их к треугольному виду.
17. 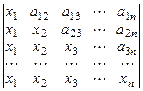 . 18.
. 18.  .
.
19.  20.
20.  .
.
Вычислить следующие определители методом рекуррентных соотношений.
21.  22.
22.  .
.
23.  . 24.
. 24. 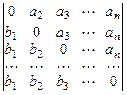 .
.
Пользуясь теоремой Лапласа вычислить следующие определители.
25.  . 26.
. 26.  . 27.
. 27.  .
.
28.  . 29.
. 29.  .
.
Вычислить определители:
30.  . 31.
. 31.  .
.
32.  . 33.
. 33. 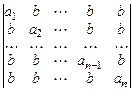 .
.
34.  .
.
35.  . 36.
. 36.  .
.
37. Порядок следующего определителя равен  :
:
 .
.
38. 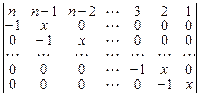 .
.
39.  . 40.
. 40.  .
.
41.  .
.
42.  .
.
Дата добавления: 2015-10-26; просмотров: 228 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке | | | Обратная матрица |