Однородные линейные системы

Общее решение однородной системы

Однородной линейной системой называется система уравнений вида

Любая однородная система совместна, так как всегда имеет нулевое (тривиальное) решение. Для существования нетривиального решения необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.

Особенностью однородной системы является то, что всякая линейная комбинация ее решений вновь является решением системы.

Определение. Если ранг матрицы равен , то всякая совокупность из линейно независимых решений называется фундаментальной системой решений.

Для отыскания общего решения системы достаточно найти ее фундаментальную систему решений и составить их линейную комбинацию

.

Фундаментальная система решений строится следующим образом. Выделяем базисную систему уравнений, главные и свободные неизвестные. Предположим, что свободными являются неизвестные . Зададим определитель 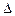порядка 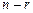, отличный от нуля

.

Принимая значения элементов го столбца определителя 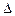за значения свободных переменных, решаем базисную систему уравнений. Получившиеся решений образуют фундаментальную систему решений. Один из возможных вариантов выбора определителя 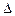состоит в задании его как определителя единичной матрицы

.

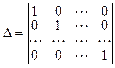Пример. Найти фундаментальную систему решений и построить общее решение системы уравнений

Приведем матрицу системы к ступенчатому виду

.

Очевидно, ранг матрицы системы равен 3, следовательно, фундаментальная система будет состоять из двух решений. За главные неизвестные можно принять , за свободные 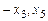. Базисная система уравнений

Задаем свободные неизвестные

Решая базисную систему, получим фундаментальные решения

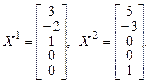
Тогда общее решение

Задачи

Найти фундаментальную систему решений и построить общее решение систем уравнений.

1. 2.

3. 4.

5.

Неоднородные системы

Дата добавления: 2015-10-26