Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке

Рассмотрим определитель матрицы

.

Выделим в этом определителе произвольный элемент , соберем в правой части равенства все члены определителя, в которые входит , и вынесем этот элемент за скобки. Величина , стоящая в скобках, называется алгебраическим дополнением элемента в определителе .

Например, в определителе третьего порядка алгебраическое дополнение элемента , а элемента .

Так как в каждый член определителя входит один и только один элемент го столбца, то можно записать, что

.

Это соотношение называется формулой разложения определителя по элементам го столбца. Аналогичная формула записывается и для любой й строки

.

Рассмотрим теперь квадратную матрицу го порядка

Выделим в этой матрице произвольные 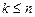строк с номерами и столько же столбцов с номерами .Элементы, стоящие на пересечении выбранных строк и столбцов образуют квадратную матрицу го порядка. Ее определитель называется минором го порядка матрицы и обозначается . Всякий элемент по определению есть минор 1-го порядка, а есть минор го порядка.

Если в исходной матрице зачеркнуть строк с номерами и столбцов с номерами , то оставшиеся элементы образуют квадратную матрицу порядка .Определитель этой матрицы называется дополнительным минором для минора . Дополнительный минор к элементу обозначается .

Например, в матрице

Миноры и алгебраические дополнения связаны между собой следующим равенством: Из формул разложения определителя по строке или столбцу получаем, что

.

Обобщением этих формул является теорема Лапласа. Пусть в определителе го порядка выделены любые столбцов с номерами . Составим всевозможные миноры го порядка из элементов, находящихся на пересечении этих столбцов и произвольных строк определителя с номерами (). Тогда

,

где . Аналогичное разложение можно записать и для произвольных строк определителя

.

Дата добавления: 2015-10-26