Основные определения. Определение 1.Системой линейных уравнений относительно неизвестных называется

Определение 1. Системой линейных уравнений относительно неизвестных называется система уравнений вида

где произвольные заданные числа – коэффициенты уравнений, 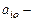свободные члены.

Если ввести матрицы

,

то систему уравнений можно записать в матричном виде

.

Матрица называется основной матрицей системы, матрица 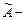расширенной матрицей системы.

Если , то система называется квадратной. Если все , система называется однородной.

Определение 2. Решением системы линейных уравнений называется всякая совокупность 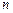чисел , которая при подстановке в систему вместо неизвестных превращает систему уравнений в систему тождеств. Система, имеющая хотя бы одно решение, называется совместной (разрешимой).

Определение 3. Всякое решение совместной системы называется ее частным решением. Совокупность всех частных решений называется общим решением.

Определение 4. Две системы уравнений называются эквивалентными, если каждое решение одной системы является решением другой.

В следующей теореме формулируется условие совместности системы линейных уравнений.

Теорема Кронекера – Копелли. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы этой системы.

Теорема (о числе решений совместной системы). Всякая совместная система уравнений с 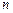неизвестными ранга при имеет единственное решение. Если , то система имеет бесконечно много решений.

Выделим в основной матрице совместной системы базисный минор.

Определение 5. Уравнения системы, соответствующие базисным строкам матрицы, называются базисными уравнениями. Их совокупность называется базисной системой уравнений. Неизвестные, коэффициенты при которых образуют базисные столбцы матрицы системы, называются главными неизвестными, остальные – свободными.

Всякая линейная система эквивалентна системе своих базисных уравнений.

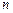При решении линейной системы, прежде всего, выделяют базисную систему. Если базисная система является совместной и состоит из уравнений с неизвестными, то далее главных неизвестных выражают через свободных.

Дата добавления: 2015-10-26