Вычисление ранга матрицы

Вычисление ранга матрицы можно проводить одним из следующих способов.

Первый состоит в сведении данной матрицы с помощью элементарных преобразований к канонической матрице. Каноническая матрица является блочной матрицей, у которой один из блоков представляет собой единичную матрицу, а все остальные блоки – нулевые матрицы.

Каноническую матрицу можно записать в виде

.

Ранг канонической матрицы равен, очевидно, числу единиц, стоящих на диагонали. Преобразования, не меняющие ранга матрицы, называются элементарными. К их числу относятся:

1. Перестановка двух любых столбцов (строк) матрицы.

2. Умножение столбца (строки) на отличное от нуля число.

3. Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).

Пример. Вычислить ранг матрицы

.

Вычтем первый столбец из четвертого и шестого, а в получившейся матрице второй столбец прибавим к четвертому, вычтем его из шестого, и удвоенный второй столбец вычтем из пятого:

.

В полученной матрице третий столбец прибавим к пятому и вычтем из четвертого

.

Далее, четвертый столбец прибавим к третьему, удвоенный четвертый столбец прибавим к пятому и шестому. Наконец, в полученной матрице вычтем третий столбец из второго, а получившийся второй из первого

.

Ранг последней матрицы равен, очевидно, 4.

Второй способ вычисления матрицы дает метод окаймления миноров, основанный на следующей теореме:

Теорема. Пусть матрица имеет минор го порядка отличный от нуля, а все миноры го порядка, содержащие (окаймляющие) его равны нулю. Тогда ранг матрицы равен .

Пример. Вычислить ранг матрицы методом окаймления миноров

.

У матрицы имеется минор второго порядка . Поэтому ранг данной матрицы не меньше двух. Окаймляют данный минор следующие миноры третьего порядка

.

Так как все они равны нулю, ранг матрицы равен двум.

Задачи

Вычислить ранг следующих матриц методом окаймления миноров.

1. . 2. .

Вычислить ранг следующих матриц при помощи элементарных преобразований.

3. . 4. .

5. Чему равен ранг матрицы

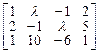
при различных значениях ?

6. Доказать, что система вектор – столбцов, содержащая нулевой вектор, линейно зависима.

7. Доказать, что если часть системы вектор – столбцов линейно зависима, то и вся система линейно зависима.

8. Найти все значения , при которых вектор – столбец 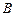линейно выражается через вектор – столбцы .

а) .

б) .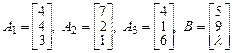

Дата добавления: 2015-10-26