
Читайте также:
|
Рассмотрим неоднородную линейную систему 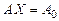 . Соответствующая ей однородная система
. Соответствующая ей однородная система 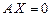 называется приведенной системой уравнений.
называется приведенной системой уравнений.
Решения неоднородной и приведенной систем связаны следующим образом. Сумма любого решения неоднородной системы и любого решения приведенной системы является решением неоднородной системы. Разность двух произвольных решений неоднородной системы есть решение приведенной системы. Поэтому общее решение неоднородной системы можно получить, прибавляя к любому ее частному решению общее решение приведенной системы
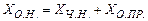 .
.
Пример 1. Найти общее решение системы уравнений
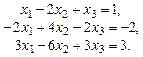
Выделим базисную систему уравнений, приведя расширенную матрицу системы к ступенчатому виду
 .
.
Так как 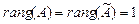 , то система совместна. Базисная система уравнений
, то система совместна. Базисная система уравнений
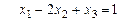 .
.
Найдем теперь частное решение неоднородной системы. Примем 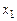 за главное, а
за главное, а 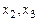 за свободные неизвестные. Положим
за свободные неизвестные. Положим 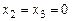 . Тогда частное решение
. Тогда частное решение
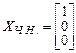 .
.
Соответствующая приведенная система имеет вид
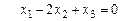 .
.
Для нахождения фундаментальной системы решений зададим значения свободных неизвестных

Тогда фундаментальные решения приведенной системы
 .
.
Откуда общее решение неоднородной системы
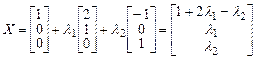 .
.
Пример 2. Исследовать систему и найти общее решение в зависимости от значения параметра 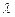 :
:
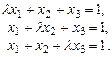
Исследование начинаем с проверки системы на совместность. Так как система является квадратной, то по теореме Крамера при  она совместна и имеет единственное решение. Для значений
она совместна и имеет единственное решение. Для значений 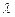 , при которых
, при которых  необходимы дополнительные исследования. Вычислим
необходимы дополнительные исследования. Вычислим 
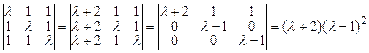 .
.
Если 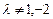 , то
, то  и решение системы находим по формулам Крамера
и решение системы находим по формулам Крамера
 .
.
Пусть  . Тогда расширенная матрица системы
. Тогда расширенная матрица системы
 .
.
Очевидно, что 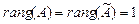 и система совместна. Базисная система уравнений
и система совместна. Базисная система уравнений
 .
.
Решая эту систему так же как в примере 1, получим общее решение
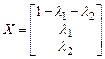 ,
,
где 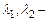 произвольные постоянные.
произвольные постоянные.
Пусть  . Преобразуем расширенную матрицу системы к ступенчатому виду
. Преобразуем расширенную матрицу системы к ступенчатому виду
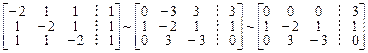 .
.
По виду первой строки ступенчатой матрицы определяем, что система несовместна.
Задачи
Исследовать системы уравнений и найти общее решение в зависимости от значений входящих в коэффициенты параметров:
1. 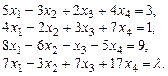 2.
2. 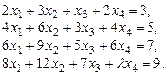
3. 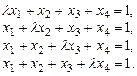 4.
4. 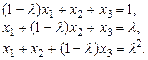
5. 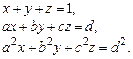 6.
6. 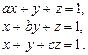
7. 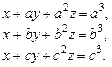 8.
8. 
9. Система

имеет единственное решение. Доказать, что 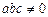 b и найти решение системы.
b и найти решение системы.
Литература
1. Воеводин В. В. Линейная алгебра. — М.: «Наука», 1974. — 400 с.
2. Ефимов Н. В., Розендрон Э. Р. Линейная алгебра и многомерная геометрия. — М.: «Наука», 1974. — 250 с.
3. Проскуряков И. В. Сборник задач по линейной алгебре. — М.: «Наука», 1970. — 355 с.
Дата добавления: 2015-10-26; просмотров: 107 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однородные линейные системы | | | THE ADVENTURES OF SHERLOCK HOLMES |