Читайте также:
|
Найдем отношение регистрируемой энергии линейчатого спектра источника 1 и энергии сплошного спектра источника 2 для данной длины волны излучения.
Рассмотрим освещение щели от исследуемого источника 1.
Введем обозначения: ∆S – площадь диафрагмы, выделяющей часть излучения (определяет ширину источника); ∆x – длина излучающего слоя. При малом давлении и малой плотности тока газоразрядная плазма практически однородна в направлении, перпендикулярном оси разряда ОО΄, поэтому ∆x определяется внутренним диаметром цилиндрического баллона лампы.
Найдем поток энергии, регистрируемый приемником излучения.
Энергия, излучаемая участком ∆S источника длиной ∆x, в пределах телесного угла 4π, за секунду равна Ιe∆S∆x. Поток энергии, посылаемый линзой 3 радиуса R, в плоскость входной щели монохроматора определяется соотношением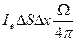 
, где 
- телесный угол, в пределах которого распространяется свет от источника.
Освещенность в плоскости входной щели 
, где ∆S¢ - площадь изображения диафрагмы ∆S. Поток энергии через площадь ∆σ – входной щели прибора найдем из соотношения 
, Учитывая, что 
, приведем формулу для потока энергии к виду
. (6)
Оптическая схема спектрального прибора дает совокупность монохроматических изображений входной щели в фокальной плоскости объектива камеры, где расположена выходная щель 5. Выходная щель должна иметь такую высоту и ширину ∆ l, чтобы была пропущена вся энергия данной длины волны, прошедшая через входную щель и оптическую систему монохроматора.
Рассмотрим освещение щели от источника сплошного спектра 2 – источника сравнения. Излучающий будет поверхность накаленного тела.
Пусть диафрагма выделяет площадь источника ∆ S. Найдем поток энергии, регистрируемый приемником излучения. Энергия, излучаемая в единственном интервале длин волн вблизи λ единицей поверхности в единицу времени в единичном телесном угле в данном направлении, определяет спектральную яркость b¢λT. Если источник косинусный, то спектральная яркость связана со спектральной светимостью тела соотношением 
.
Энергия, передаваемая линзой в плоскость входной щели монохроматора, определяется соотношением 
, а освещенность щели - соотношением 
.
Сделав преобразования, как в предыдущем случае, найдем поток лучистой энергии, прошедший в спектральный прибор
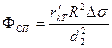
Согласно закону Кирхгофа 
, где 
– спектральная светимость абсолютно черного тела, α¢λT – спектральная поглощательная способность серого тела при температуре Т для данной длины волны λ. Поток лучистой энергии будет равен
.
Поток энергии, перенесенной через выходную щель прибора и зарегистрированной приемником излучения, зависит от ширины выходной щели ∆l, выделяющий участок сплошного спектра, и линейной дисперсии монохроматора 
:
, (7)
где 
- величина, обратная линейной дисперсии; ∆l – интервал длин волн, выделяемый выходной щелью.
Найдем отношение регистрируемого потока энергии Ф (6) линейчатого спектра к потоку энергии ФСП (7) сплошного спектра для данной длины волны, обозначив это отношение Кλ:
.
Подставив Ιe, найденное из последнего соотношения, в формулу 
, получим формулу для определения концентрации атомов в возбужденном состоянии:
, (8)
Итак, для определения концентрации атомов в возбужденном состоянии ni необходимо экспериментально найти К λ и 
.
При фотоэлектрической регистрации излучения показания прибора, регистрирующего фототок, пропорциональны величине потока излучения, вызвавшего этот фототок. Поэтому 
, где К – число делений регистрирующего фототок прибора при освещении щели от источника излучения 1, КСП – число делений при освещении щели от источника сравнения 2 для той же длины волны излучения, при той же ширине выходной щели ∆l.
В таблице приведены значения спектральной излучательной способности абсолютно черного тела для длин волн, равных длинам волн триплета атомов ртути, при различных значениях температуры тела. Зная α¢λT и Т, пользуясь таблицей, можно найти . Для вольфрама в видимой области спектра α¢λT = 0,44 при Т ≈ 2000 К.
| Т, К | l = 546 нм | l = 435,8 нм | l = 404,6 нм |
| , Дж⁄м3с
| , Дж⁄м3с
| , Дж⁄м3с
| |
| 5,5 ∙108 | 3,0 ∙107 | 8,6 ∙106 | |
| 1,3 ∙109 | 1,0 ∙108 | 1,7 ∙107 | |
| 3,5∙ 109 | 3,0 ∙108 | 9,0 ∙107 | |
| 5,6∙ 109 | 6,3 ∙108 | 1,3 ∙108 | |
| 2,0 ∙1010 | 1,7 ∙109 | 6,7 ∙108 | |
| 4,0 ∙1010 | 4,0 ∙109 | 1,0 ∙109 | |
| 4,9 ∙1010 | 8,0∙ 109 | 3,5 ∙109 | |
| 1,6 ∙1011 | 2,0 ∙1010 | 5,6 ∙109 | |
| 2,5 ∙1011 | 2,6 ∙1010 | 1,4 ∙1010 |
Для определения температуры вольфрамовой нити лампы сравнения 2 использован бесконтактный оптический метод. Приборы, служащие для определения температуры на основе регистрации теплового излучения, называют оптическими пирометрами. В оптических пирометрах одна из характеристик излучения нагретого тела сравнивается с соответствующей характеристикой излучения абсолютно черного тела. В работе использован яркостный пирометр (пирометр с исчезающей нитью) (см. приложение 2).Он позволяет визуально сравнить яркость изображения нагретого тела и яркость дугообразной нити лампы, вмонтированной в пирометр и прокалиброванный по излучению абсолютно черного тела при различных значениях его температуры.
С помощью яркостного пирометра определяют яркостную температуру исследуемого нагретого тела Тя. Она ниже его истинной термодинамической температуры Т. В работе для перехода от Тя к Т нужно воспользоваться графиком (рис. 3).
|
 |
Дата добавления: 2015-10-24; просмотров: 174 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оптический метод диагностики низкотемпературной плазмы | | | Сущность опытов, проведенных Дж. Франком и Г. Герцем. |