
Читайте также:
|
Рассматриваем линейное пространство Е над полем вещественных чисел R. Скалярным произведением векторов a и b называется число 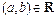 , если
, если
1) 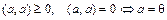 ;
;
2) 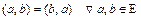 ;
;
3)  ;
;
4) 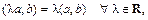
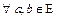 .
.
Евклидовым пространством называется линейное пространство Е с введенным на нем скалярным произведением.
Скалярное произведение представляет собой вещественнозначную функцию от двух переменных, определенных на Е. Условия 3) и 4) говорят о том, что функция линейна по первой переменной. Из условия 2) легко следует линейность и по второй переменной. В самом деле:
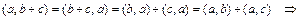
 .
.
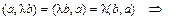
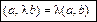 .
.
Свойства скалярного произведения:
1) 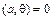 ;
;
2) 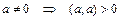 ;
;
3) 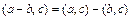 .
.
Доказательство свойства 1).
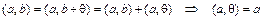 .
.
Доказательство свойства 3).
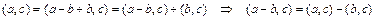 .
.
Теорема (неравенство Коши – Буняковского)
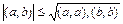 .
.
Доказательство. Если 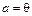 или
или 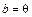 , то неравенство выполняется. Будем считать
, то неравенство выполняется. Будем считать  .
.
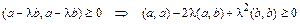 .
.
Так как 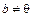 , то квадратный трехчлен в левой части неравенства принимает значения
, то квадратный трехчлен в левой части неравенства принимает значения 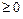 , если дискриминант неположителен, т.е.
, если дискриминант неположителен, т.е. 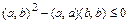 ,
, 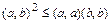 .
.
Введем обозначение  и назовем это число нормой вектора или длиной. Вектор
и назовем это число нормой вектора или длиной. Вектор  для ненулевого вектора а назовем ортом вектора а. Переход
для ненулевого вектора а назовем ортом вектора а. Переход 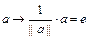 называется нормированием. Заметим, что
называется нормированием. Заметим, что 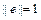 . Для ненулевых векторов а и b из неравенства Коши – Буняковского следует, что
. Для ненулевых векторов а и b из неравенства Коши – Буняковского следует, что 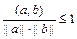 . ■
. ■
Существует угол 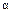 , для которого
, для которого 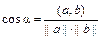 ;
; 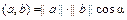 . Будем называть
. Будем называть 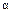 углом между векторами а и b. Векторы а и b называются ортонормированными, если их скалярное произведение равно нулю:
углом между векторами а и b. Векторы а и b называются ортонормированными, если их скалярное произведение равно нулю:  . Считаем, что нулевой вектор
. Считаем, что нулевой вектор 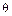 ортогонален любому. Система векторов называется ортогональной, если ее векторы попарно ортогональны.
ортогонален любому. Система векторов называется ортогональной, если ее векторы попарно ортогональны.
Теорема. Ортогональная система ненулевых векторов линейно независима.
Доказательство. Для ортогональной системы ненулевых векторов 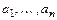 запишем
запишем 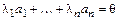 . Домножим скалярно обе части равенства на
. Домножим скалярно обе части равенства на 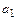 . Получим
. Получим
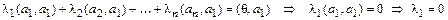 .
.
Аналогично проверяется, что 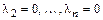 . ■
. ■
Базис 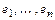 называется ортонормированным, если он ортогонален и каждый его вектор нормирован, т.е.
называется ортонормированным, если он ортогонален и каждый его вектор нормирован, т.е.
 .
.
Теорема. Скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат.
Доказательство. 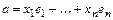 ,
, 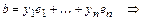
 . ■
. ■
Квадратная матрица А порядка n называется ортогональной, если  , где
, где 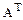 – транспонированная матрица, I – единичная матрица порядка n.
– транспонированная матрица, I – единичная матрица порядка n.
Теорема. Матрица перехода от одного ортонормированного базиса к другому ортогональна.
Доказательство. 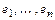 и
и 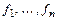 – два ортонормированных базиса,
– два ортонормированных базиса,
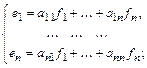
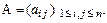
Тогда с одной стороны  для
для 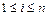 , а с другой стороны
, а с другой стороны 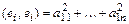 , т.е.
, т.е. 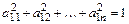 .
.
С одной стороны 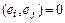 для
для 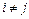 , а с другой стороны
, а с другой стороны  , т. е.
, т. е. 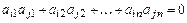 . Отсюда
. Отсюда  . ■
. ■
Теорема. В любой линейной оболочке  существует ортогональный базис.
существует ортогональный базис.
Доказательство. Построим новую систему образующих линейной оболочки следующим образом:
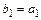 ,
,
 ;
;
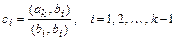 , если
, если 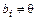
и 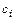 – любое число, если
– любое число, если 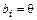 .
.
Значения 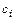 получены из условия
получены из условия 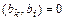 . Система
. Система 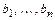 ортогональна по построению и является системой образующих, так как все векторы
ортогональна по построению и является системой образующих, так как все векторы 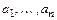 линейно выражаются через
линейно выражаются через 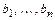 . ■
. ■
Процессом ортогонализации системы 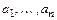 называется переход к системе
называется переход к системе 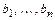 .
.
Пример. Применить процесс ортогонализации к системе
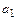 =(1, 1, -1, -2),
=(1, 1, -1, -2), 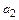 =(5, 8, -2, -3),
=(5, 8, -2, -3), 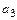 =(3, 9, 3, 8).
=(3, 9, 3, 8).
Ў 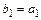 . Вектор
. Вектор 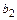 ищем в виде
ищем в виде 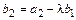 , где
, где 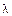 находим из условия
находим из условия 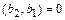 , т.е.
, т.е. 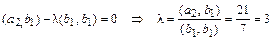 ,
,  =(5, 8, -2, -3) – 3(1, 1, -1, -2)=(2, 5, 1, 3).
=(5, 8, -2, -3) – 3(1, 1, -1, -2)=(2, 5, 1, 3).
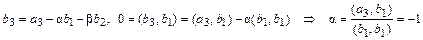 ,
,
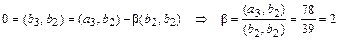 ;
;
 (3, 9, 3, 8)+(1, 1, -1, -2) – 2(2, 5, 1, 3)=(0, 0, 0, 0).
(3, 9, 3, 8)+(1, 1, -1, -2) – 2(2, 5, 1, 3)=(0, 0, 0, 0).
Ответ:  =(1, 1, -1, -2),
=(1, 1, -1, -2), 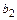 =(2, 5, 1, 3). Вектор
=(2, 5, 1, 3). Вектор 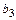 оказался нулевым из – за того, что векторы
оказался нулевым из – за того, что векторы 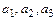 линейно зависимы. Рациональнее было бы в начале выделить максимальную линейно независимую подсистему и уже к ней применить процесс ортогонализации.
линейно зависимы. Рациональнее было бы в начале выделить максимальную линейно независимую подсистему и уже к ней применить процесс ортогонализации.
Комплексным евклидовым пространством или унитарным называется линейное пространство над полем комплексных чисел, в котором каждой паре а и b векторов поставлено в соответствие комплексное число (a, b), удовлетворяющее условиям:
1) 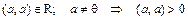 ;
;
2) 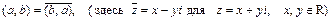 ;
;
3) 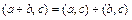 ;
;
4) 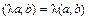 .
.
Свойства скалярного произведения, определенного в комплексном евклидовом пространстве:
1)  ;
;
2) 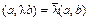 .
.
Доказательство: (1).  .
.
Доказательство: (2). 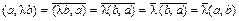 .
.
В комплексном евклидовом пространстве также имеет место неравенство Коши – Буняковского, точно также определяются понятия ортогональности, ортонормированного базиса и т.п.
Упражнения
1) Построить ортогональный базис подпространства, натянутого на векторы 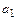 =(1, 2, 2, -1),
=(1, 2, 2, -1), 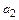 =(1, 1, -5, 3),
=(1, 1, -5, 3), 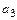 =(3, 2, 8, -7).
=(3, 2, 8, -7).
2) Пусть 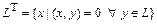 (ортогональное дополнение подпространства L евклидова пространства Е). Доказать, что
(ортогональное дополнение подпространства L евклидова пространства Е). Доказать, что
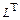 – подпространство евклидова пространства Е;
– подпространство евклидова пространства Е;
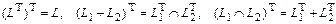 ;
;
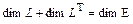 .
.
3) Доказать, что скалярное произведение двух векторов комплексного евклидова пространства, заданных координатами в ортонормированном базисе, вычисляется по формуле 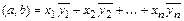 .
.
Дата добавления: 2015-10-23; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямая сумма подпространств | | | Глава 3.2. Системы линейных уравнений |