Прямая сумма подпространств

Пусть, , 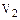…, – подпространства линейного пространства . Суммой подпространств называется множество всех сумм элементов этих подпространств, взятых по одному из каждого подпространства:

Теорема.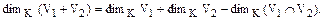

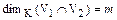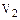Доказательство. Пусть – базис , т. е. . Элементы линейно независимы в и их можно в дополнить до максимальной линейно независимой системы, т.е. до базиса : – базис , . Аналогично, дополним систему до базиса : - базис 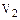, . Векторы линейно независимы. В самом деле, если

,

то

.

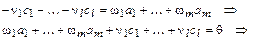
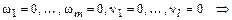
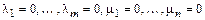Итак, из того, что линейная комбинация этих векторов равна 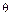, следует, что все коэффициенты равны нулю, а это и означает их линейную независимость. Ясно, что эти векторы – система образующих подпространства , а значит, базис. Получили, что

■

Сумма подпространств называется прямой, если каждый её элемент можно представить в виде суммы элементов подпространств единственным образом. В этом случае пишут … .

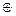
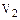
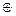Теорема. Сумма + … + – прямая

, i =1,..., k.

Доказательство.

Дано: сумма + … + – прямая. Без ограничения общности можно рассмотреть лишь случай i =1.

Пусть .

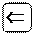Тогда , где 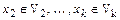, т.е. . С другой стороны, для нулевого вектора уже существует представление в виде суммы элементов подпространств: 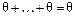. В силу единственности представления получаем 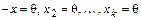, т.е. .

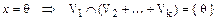Дано: .

Предположим, что для некоторого элемента х имеем где . Аналогично доказывается, что . Следовательно, любой элемент представим в виде суммы элементов единственным образом.

Если , то говорят, что линейное пространство разложимо в прямую сумму подпространств. В этом случае и каждый элемент представим в виде суммы элементов из и притом единственным образом.

Если 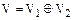, то подпространства и 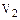называются дополнительными.

Пусть и 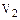– произвольные линейные пространства над одним и тем же полем К. Рассмотрим множество пар вида 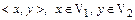. Оно является линейным пространством (надо проверить!) относительно отношения

равенства ,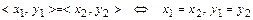

сложения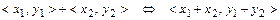

и умножения на элемент поля .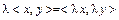

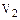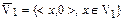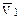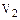Это линейное пространство называется (внешней) прямой суммой линейных пространств и . Заметим, что изоморфно подпространству , а , т.е. . Обычно отождествляют и , и . При таком отождествлении внешняя прямая сумма совпадает с введенной ранее внутренней прямой суммой. ■

Упражнения

1) Для подпространств и 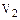докажите, что и тоже подпространства линейного пространства .

2) Докажите, что 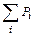семейства подпространств – линейная оболочка их объединения.

3) Докажите, что сумма и 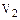– прямая .

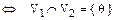4) Докажите, что сумма 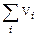– прямая тогда и только тогда, когда нулевой вектор представим в виде суммы элементов подпространств единственным образом.

5) Если , то , где , , 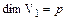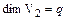. Докажите.

6) Если 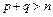, то 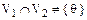. Докажите.

7) Для любого подпространства существует дополнительное подпространство. Докажите.

Дата добавления: 2015-10-23