Фундаментальная система решений

Соотношения

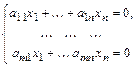(2)

образуют однородную систему 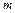линейных уравнений от неизвестных, .

Будем записывать решения системы линейных уравнений в виде векторов .

Теорема. Совокупность всех решений однородной системы линейных уравнений = подпространство линейного пространства строк .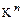

Доказательство. Система совместна, так как имеет нулевой ранг. Очевидно, что сумма двух решений – вновь решения этой системы; произведение решения на элемент 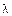– вновь решение. Следовательно, множество всех решений само образует линейное пространство над полем К. ■

Теорема. Размерность линейного пространства решений однородной системы линейных уравнений равна разности между числом неизвестных и рангом матрицы системы.

Доказательство. Пусть 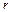– ранг матрицы системы. Без ограничения общности рассуждений можно считать, что базисный минор располагается в левом верхнем углу матрицы. Разрешив систему относительно первых 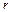переменных, получим

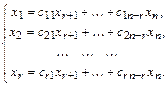
Придавая свободным переменным нулевые значения всем, кроме одной, получим решения

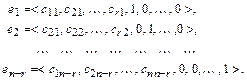
Эти решения линейно независимы.

Если – произвольное решение системы (1), то

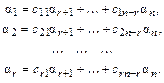
Отсюда,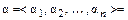

.

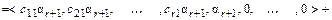
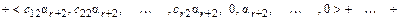
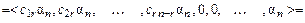
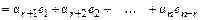Векторы 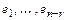образуют базис линейного пространства решений, поэтому его размерность равна . ■

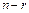Базис линейного пространства решений однородной системы линейных уравнений называют фундаментальной совокупностью решений (кратко ФСР). Если 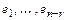– ФСР, то – решение системы (2) при любых 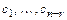из поля К, которое будем называть общим решением системы (2). ФСР, найденную в процессе доказательства теоремы, называют нормальной.

Теорема. Общее решение Х неоднородной системы линейных уравнений (1) имеет вид

,

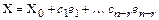где 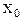– некоторое решение системы (1), а 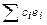– общее решение соответствующей однородной системы линейных уравнений.

Доказательство. 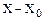– решение системы (2) и его можно записать в виде . ■

Пример. Найти ФСР и общее решение системы

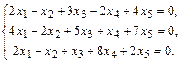
Решение.

~ ~ .

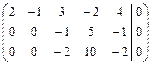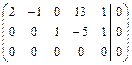Исходная система равносильна такой

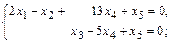
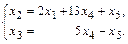
Придадим свободным переменным 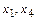и значения 1, 0, 0; затем 0, 1, 0; а затем 0, 0, 1. Получим ФСР системы

= < 1, 2, 0, 0, 0 >,

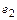= < 0, 13, 5, 1, 0 >,

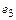= < 0, 1, -1, 0, 1 >.

Общее решение системы:

.

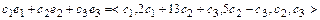Упражнения

1) Найдите ФСР и общее решение однородной системы линейных уравнений

а) б)

в)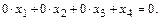

2) Почему в каждом решении системы

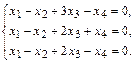
Контрольная работа №5 по теме “Линейные пространства. Системы линейных уравнений”

Задание 1. Показать, что векторы , , образуют базис и найти координаты вектора 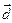в этом базисе.

1) = (-3, 4, 7), = (0, -8, 11), = (13, 1, 5), 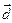= (-19, -1, 20).

2) = (4, 0, 9), = (10, -7, 2), = (-1, 1, 14), = (-25, 20, -11).

3) = (-8, 13, -7), = (-3, 1, -7), = (4, -3, 3), = (11, 0, 19).

4) = (-4, 17, 3), = (-2, 0, 2), = (12, 6, 5), = (-20, 11, 2).

5) = (2, -3, 14), = (7, 0, -8), = (11, 13, 0), = (-6, 7, 52).

6) = (15, -1, 0), = (4, 7, -11), = (-1, -2, 3), = (-9, 12, -17).

7) = (-4, 11, 9), = (1, -2, 0), = (-3, 2, -1), = (-12, 19, 7).

8) = (-1, 16, 7), = (0, 3, -7), = (3, 4, -5), = (-2, -23, 5).

9) = (0, -13, 2), = (8, 5, -7), = (-1, -1, 4), = (7, 30, -7).

10) = (-3, -7,4), = (12, -1, 0), = (-2, 2, 11), = (3, -2, 37).

11) = (-11, 7,0), = (2, 2, 5), = (-3, -6, 1), = (4, -17, -9).

12) = (2, 14,-1), = (7, 0, 3), = (9, 1, 1), = (-12, 27, -6).

13) = (3, -9,3), = (0, 4, 11), = (17, 1, -1), = (20, 0, 24).

14) = (-7, 11,0), = (1, -5, 7), = (3, 3, -5), = (-25, 35, -2).

15) = (0, 18,3), = (-7, 1, -2), = (1, 9, 5), = (-4, -8, 7).

16) = (11, -5,3), = (4, -6, 0), = (-7, 7, 2), = (17, -7, -1).

17) = (5, -13,2), = (7, 0, 4), = (-3, -1, 6), = (-16, 14, -16).

18) = (-3, 4, 0), = (17, 2, -11), = (7, 5, -7), = (4, 5, -4).

19) = (0, 4, -18), = (5, -3, 6), = (1, -11, -5, = (-3, -11, -32).

20) = (-7, 9, 2), = (10, 0, -6), = (3, -1, 8), = (30, -10, -6).

21) = (12, -1, 0), = (3, 7, -2), = (-1, 5, 15), = (14, 11, 13).

22) = (2, 17, -5), = (4, 8, 0), = (1, 10, -1), = (-3, 5, 2).

23) = (3, -8, 0), = (12, -7, -4), = (2, 1, -2), = (-5, -18, 8).

24) = (7, -8, 3), = (10, 0, -15), = (4, -5, 8), = (-27, -3, 40).

25) = (-3, -1, 6), = (7, 0, 4), = (5, -13, 2), = (0, 27, -6).

26) = (-7, 7, 2), = (4, -6, 0), = (11, -5, 3), = (14, -22, -9).

27) = (1, 9, 5), = (-7, 1, -2), = (0, 18, 3), = (-9, -35, -15).

28) = (3, 3, -5), = (1, -5, 7), = (-7, 11, 0), = (18, -24, 2).

29) = (17, 1, -1), = (0, 4, 11), = (3, -9, 3), = (-23, 21, 6).

30) = (9, 1, 1), = (7, 0, 3), = (2, 14, -1), = (30, -25, 8).

Задание 2. Даны два базиса пространства строк: 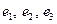и 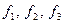. Найти:

а) матрицу А перехода от базиса 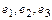к базису ;

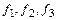б) матрицу обратного перехода;

в) координаты в обоих базисах;

г) координаты вектора 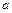в базисе 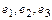, имеющего во втором базисе координаты (1, 1, 1).

1)

2)

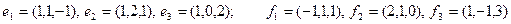
3)

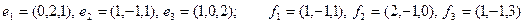
4)

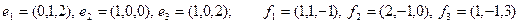
5)

6)

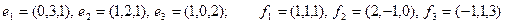
7)

8)

9)

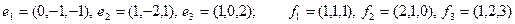
10)

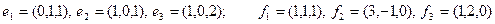
11)

12)

13)

14)

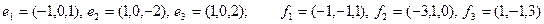
15)

16)

17)

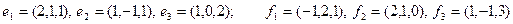
18)

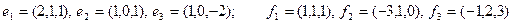
19)

20)

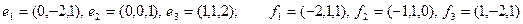
21)

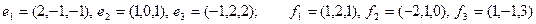
22)

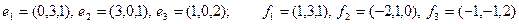
23)

24)

25)

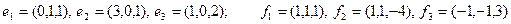
26)

27)

28)

29)

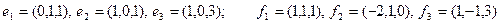
30)

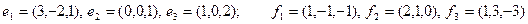
Задание 3. Применить процесс ортогонализации к системе векторов.

1)

2)

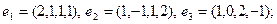
3)

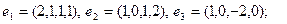
4)

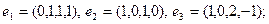
5)

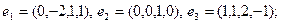
6)

7)

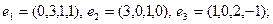
8)

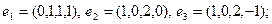
9)

10)

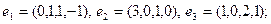
11)

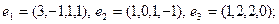
12)

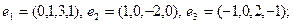
13)

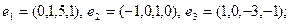
14)

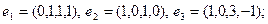
15)

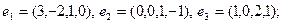
16)

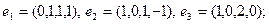
17)

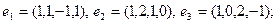
18)

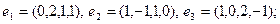
19)

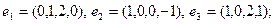
20)

21)

22)

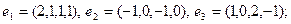
23)

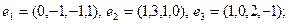
24)

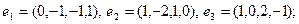
25)

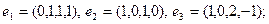
26)

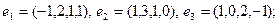
27)

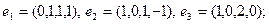
28)

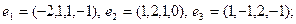
29)

30)

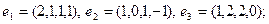
Задание 4. Решить систему линейных уравнений: 1) методом Гаусса; 2) по формулам Крамера; 3) матричным методом.

1)

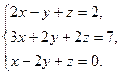
2)

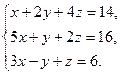
3)

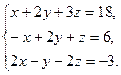
4)

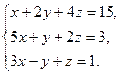
5)

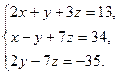
6)

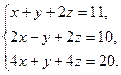
7)

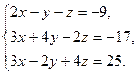
8)

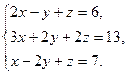
9)

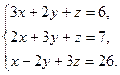
10)

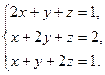
11)

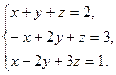
12)

13)

14)

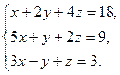
15)

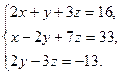
16)

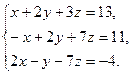
17)

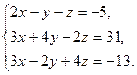
18)

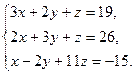
19)

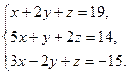
20)

21)

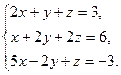
22)

23)

24)

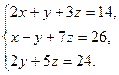
25)

26)

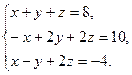
27)

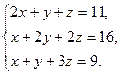
28)

29)

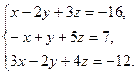
30)

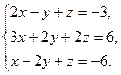
Задание 4. Исследовать совместность данной системы и, в случае ее совместности, найти общее решение и одно частное решение.

1)

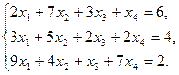
2)

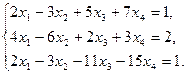
3)

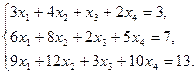
4)

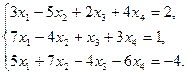
5)

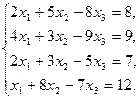
6)

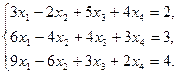
7)

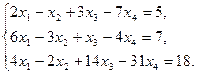
8)

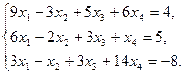
9)

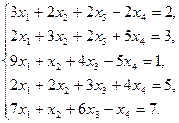
10)

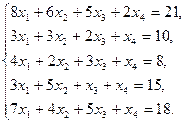
11)

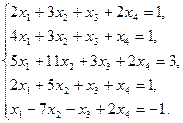
12)

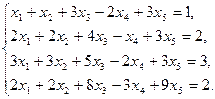
13)

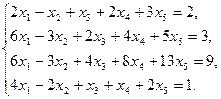
14)

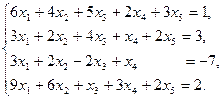
15)

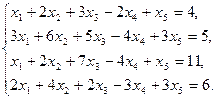
16)

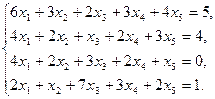
17)

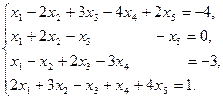
18)

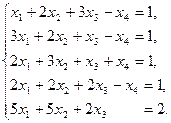
19)

20)

21)

22)

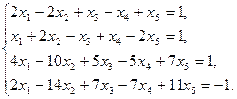
23)

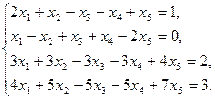
24)

25)

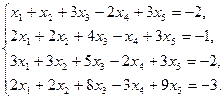
26)

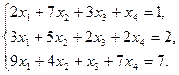
27)

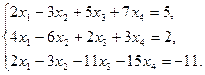
28)

29)

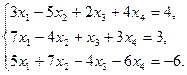
30)

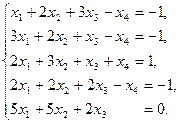
Задание 6. Найти общее решение однородной системы линейных уравнений и фундаментальную систему решений.

1)

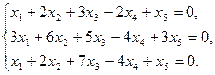
2)

3)

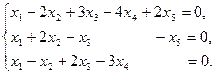
4)

5)

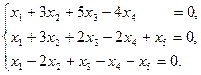
6)

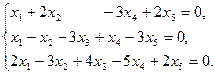
7)

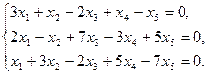
8)

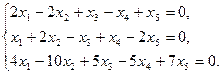
9)

10)

11)

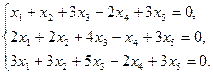
12)

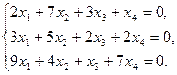
13)

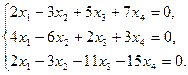
14)

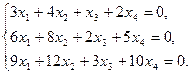
15)

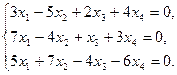
16)

17)

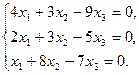
18)

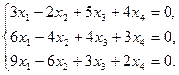
19)

20)

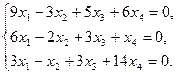
21)

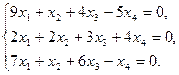
22)

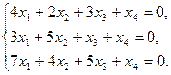
23)

24)

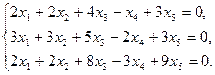
25)

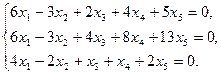
26)

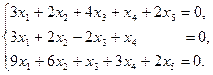
27)

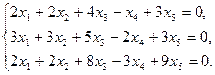
28)

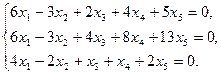
29)

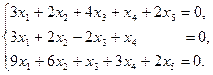
30)

Дата добавления: 2015-10-23