
Читайте также:
|
Два линейных пространства V1 и V2 над полем К называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие 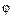 , для которого
, для которого
1) 

2) 
Отображение  в этом случае называется изоморфизмом, а для линейных пространств применяется обозначение
в этом случае называется изоморфизмом, а для линейных пространств применяется обозначение  .
.
Для того, чтобы проверить является ли отображение  изоморфизмом линейных пространств в соответствии с этим определением, надо убедиться, что
изоморфизмом линейных пространств в соответствии с этим определением, надо убедиться, что
1) 
2)  – сюръекция, т.е.
– сюръекция, т.е. 
3)  – линейное отображение, т.е.
– линейное отображение, т.е.  и
и 
Свойства изоморфизмов:
1) 
2)  где
где  и
и  – нулевые векторы
– нулевые векторы  и
и 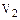 соответственно.
соответственно.
3) 
4) 
Теорема. При изоморфизме линейно независимая система переходит в линейно независимую.
Доказательство. Пусть  – изоморфизм между линейными пространствами
– изоморфизм между линейными пространствами  и
и 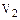 над полем К и
над полем К и 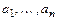 линейно независимы в
линейно независимы в  . Предположим, что
. Предположим, что  и
и  – нулевые векторы
– нулевые векторы  и
и 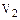 соответственно и
соответственно и 
Тогда по свойству линейности  , а в силу того, что
, а в силу того, что  – мономорфизм,
– мономорфизм,  . Из линейной независимости взятых векторов следует, что
. Из линейной независимости взятых векторов следует, что  Это означает, что векторы
Это означает, что векторы  линейно независимы. ■
линейно независимы. ■
Теорема. Все линейные пространства одной и той же размерности изоморфны между собой.
Доказательство. Пусть  и
и 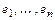 базис
базис  . Любой вектор
. Любой вектор  можно разложить по базису:
можно разложить по базису:  .
.
Докажем, что 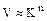 . Для этого проверим, что отображение
. Для этого проверим, что отображение  – инъекция, сюръекция и линейное. Соответствие
– инъекция, сюръекция и линейное. Соответствие  действительно отображает
действительно отображает  в
в 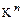 , так как каждому вектору в фиксированном базисе ставится в соответствие единственный набор коэффициентов. Если векторы различны, то хотя бы в одной координате они отличаются, поэтому
, так как каждому вектору в фиксированном базисе ставится в соответствие единственный набор коэффициентов. Если векторы различны, то хотя бы в одной координате они отличаются, поэтому  – инъекция. Если
– инъекция. Если  , то в
, то в  существует элемент
существует элемент  и при этом
и при этом  , т.е.
, т.е.  – сюръекция. Столь же очевидна и линейность отображения
– сюръекция. Столь же очевидна и линейность отображения  . Если
. Если  ,
,  , то
, то  и
и  , т. е.
, т. е.  ,
,  .
.
Так как все линейные пространства над К изоморфны 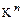 , то они изоморфны между собой. ■
, то они изоморфны между собой. ■
Замечание. Изоморфизм как бы “срисовывает” структуру линейного пространства. Поэтому утверждение теоремы можно трактовать так: линейные пространства одной и той же размерности с алгебраической точки зрения тождественны.
Упражнения
1) Линейно ли отображение  , если
, если
а)  ;
;
б)  ;
;
в)  .
.
2) Если  – линейное отображение
– линейное отображение  в
в 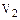 , то
, то  называется гомоморфным отображением,
называется гомоморфным отображением, 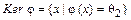 ,
,  . Докажите, что
. Докажите, что  – подпространство линейного пространства
– подпространство линейного пространства  , Im
, Im  – подпространство линейного пространства
– подпространство линейного пространства 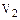 .
.
3) Линейное инъективное отображение  в
в 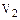 называется мономорфизмом. Докажите, что если
называется мономорфизмом. Докажите, что если  – мономорфизм, то
– мономорфизм, то  .
.
4) Линейное сюръективное отображение  на
на 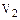 называется эпиморфизмом. Докажите, что если
называется эпиморфизмом. Докажите, что если  эпиморфизм
эпиморфизм  , то
, то  .
.
Дата добавления: 2015-10-23; просмотров: 347 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Матрица перехода от базиса к базису | | | Прямая сумма подпространств |