Интерполяционный полином Лагранжа.

Исходя из однозначности интерполяционного многочлена φ(x), можно построить полином в канонической форме, коэффициенты которого определяются из системы линейных алгебраических уравнений. Обозначим заданные значения f(x_i) = y_i. Поскольку искомый полином φ(x) должен принимать в заданных узлах х₀, х_і,...,х_n значения, которые совпадают со значениями f(х₀), f(х_і),..., f(х_n), можно записать φ(x) в виде:

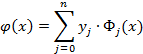
где Ф_j(x) — многочлен степени n, который в узлах интерполяции удовлетворяет такому условию:

Данный вариант записи интерполяционного многочлена φ(x) называют интерполяционным полиномом Лагранжа. Для поиска Ф_j(x) находят многочлен степени n, который равняется нулю в узлах интерполяции х_і (і = 0,1,..., j-1, j+1,..., n) и равняется единице в точке x_i. Многочлен, который удовлетворяет этим требованиям, может быть записан в виде:

Тогда интерполяционный полином в форме Лагранжа может быть записан в виде

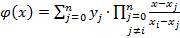(3.5)

Этот полином имеет специальное обозначение – L_n(x).

Старшая степень аргумента х в полиноме Лагранжа равна n, так как каждое произведение в формуле (3.5) содержит n сомножителей (х- х_і). В узлах х= х_і, выполняются условия Лагранжа, потому что в сумме (3.5) остается по одному слагаемому остальные обращаются в нуль за счет нулевых сомножителей в произведениях.

Пример 4.1. Пусть функция задана значениями в таблице. Для данного случая, когда мы имеем четыре значения функции, интерполяционная формула Лагранжа представляется так:

x	y
	5,6
	6,7
	8,1
	10,3

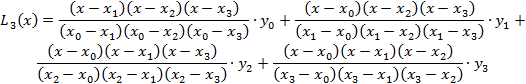
После подстановки заданных значений в формулу Лагранжа получаем:

Пример 4.2. Пример в Matlab.

% Построить интерполяционный многочлен Лагранжа

% Введём табличную функцию

x = [-1 0 1 2];

y = [4 2 0 1];

% Построим интерполяционный многочлен (аппроксимация четвёртой степени)
p = polyfit(x, y, 4);

% Коэффициенты интерполяционного интерполяции

p

>>

p =
	1.2500	-2.0000	-1.2500		2.0000

В отличие от канонического интерполяционного полинома для вычисления значений полинома Лагранжа не требуется предварительного определения коэффициентов полинома путем решения системы уравнений. Однако для каждого значения аргумента х полином (3.5) приходится пересчитывать вновь, коэффициенты же канонического полинома вычисляются только один раз. С известными коэффициентами для вычисления значений канонического полинома требуется значительно меньшее количество арифметических операций по сравнению с полиномом Лагранжа. Поэтому практическое применение полинома Лагранжа оправдано только в случае, когда интерполяционная функция вычисляется в сравнительно небольшом количестве точек х. Важное место занимает полином Лагранжа в теории численных методов.

Другой метод построения интерполяционного полинома – использование метода Ньютона.

Интерполяционный полином Ньютона. Ошибки интерполяции. Темы на самостоятельное изучение.

Дата добавления: 2015-10-29