Интерполяционный многочлен Лагранжа

Пусть функция y=f(x) задана таблицей (*). Построим интерполяционный многочлен L_n(x) степень которого не больше n, и выполняются условия (3.1): L_n(x_i)=y_i, i=0, 1, …, n

Будем искать L_n(x) в виде , где p_i(x) многочлен степени n и , т.е. p_i(x) только в одной точке отличен от нуля при i=j, а остальных точках он обращается в нуль. Следовательно, все эти точки являются для него корнями:

p_i(x)=c(x-x₀)(x-x₁)…(x-x_i-1)(x-x_i+1)…(x-x_n)

при x=x_i

p_i(x_i)=c(x_i-x₀)(x_i-x₁)…(x_i-x_i-1)(x_i-x_i+1)…(x_i-x_n)

1=c(x_i-x₀)(x_i-x₁)…(x_i-x_i-1)(x_i-x_i+1)…(x_i-x_n)

c=[(x_i-x₀)(x_i-x₁)…(x_i-x_i-1)(x_i-x_i+1)…(x_i-x_n)]^-1

подставим с в формулу p_i(x), получим

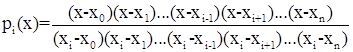
отсюда

(3.2)

Это и есть интерполяционный многочлен Лагранжа. По таблице (*) формула (3.2) позволяет весьма просто составить внешний вид многочлена.

x	x0	x1
y	y0	y1
x
y

Пример 1.

N=1 (два узла интерполяции)

– уравнение прямой, проходящей через точки (x₀, y₀), (x₁, y₁)

Пример 2.

N=2 (три узла интерполяции)

x	x0	x1	x2
y	y0	y1	y2
x
y

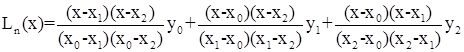– уравнение параболы, проходящей через точки (x₀, y₀), (x₁, y₁), (x₂, y₂)

Построим график этой функции и отметим на нем узловые точки M_i(x_i, y_i)

Рис 3.1

Задача 1.

Найти приближенное значение функции f(arg) при данном значении аргумента arg с помощью интерполяционного многочлена Лагранжа, если функция задана таблицей.

x	x0	x1	…	xn
y	y0	y1	…	yn

arg=…

Алгоритм:

{Программа 3.1}

program Lagrange;

uses Crt;

var X, Y: array[1..100] of Real;

Arg, L, F: Real; I, J, N:Integer;

begin

Write('Введите количество узлов интерполяции');

Readln(n);

WriteLn('Введите таблицу значений xi, yi');

for I:=0 to N do begin

Write('X[',I,']='); ReadLn(X[I]);

Write('Y[',I,']='); ReadLn(Y[I]);

end;

Write('Введите аргумент '); ReadLn(Arg);

L:=0;

For I:=0 to N do begin

F:=1;

for J:=0 to N do

if I<>J then F:=F*(Arg-X[J])/(X[I]-X[J]);

F:=F*Y[I]; L:=L+F;

end;

WriteLn('Значение многочлена Лагранжа в точке ',Arg:0:3);

WriteLn('равно ', L:0:3); ReadLn;

end.

Задача 2.

x	x0	x1	x2
y	y0	y1	y2

По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа, построить график и отметить на нем узловые точки.

Решение: см. выше пример 2.

Варианты самостоятельных работ для задачи 1 и задачи 2 см. Приложение 2

Дата добавления: 2015-10-31