Вычисление приближенного значения функции с помощью электронных таблиц

Напомним формулу интерполяционного многочлена Лагранжа:

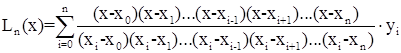
Введем обозначения:

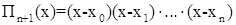
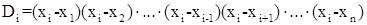
тогда 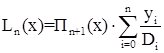(3.3)

По этой формуле удобно вычислять многочлен Лагранжа L_n(x) в таблице.

Пример 3

Пусть требуется вычислить значение многочлена Лагранжа L_n(x) в точке х. Тогда необходимо составить следующую таблицу:

i	xi	Разности	yi	Di	yi/Di
	x0	(x-x0)	(x0-x1)	(x0-x2)	(x0-x3)	(x0-x4)	(x0-x5)	y0	…	…
	x1	(x1-x0)	(x-x1)	(x1-x2)	(x1-x3)	(x1-x4)	(x1-x5)	y1	…	…
	x2	(x2-x0)	(x2-x1)	(x-x2)	(x2-x3)	(x2-x4)	(x2-x5)	y2	…	…
	x3	(x3-x0)	(x3-x1)	(x3-x2)	(x-x3)	(x3-x4)	(x3-x5)	y3	…	…
	x4	(x4-x0)	(x4-x1)	(x4-x2)	(x4-x3)	(x-x4)	(x4-x5)	y4	…	…
	x5	(x5-x0)	(x5-x1)	(x5-x2)	(x5-x3)	(x5-x4)	(x-x5)	y5	…	…

Далее необходимо вычислить (это произведение подчеркнутых разностей) и сумму последнего столбца 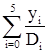. Тогда получаем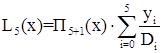

Задача 3

Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана своей таблицей. Вычислить значение функции F(х) при х=0,263

x	0,05	0,10	0,17	0,25	0,30	0,36
y	0,050042	0,100335	0,171657	0,255342	0,309336	0,376403

Воспользовавшись формулой (3.3) составим таблицу разностей

0,263
i	xi	Разности	yi	Di	Yi/Di
	0,05	0,213	-0,05	-0,12	-0,2	-0,25	-0,31	0,050042	-2E-05	-2526,23
	0,1	0,05	0,163	-0,07	-0,15	-0,2	-0,26	0,100335	4,45E-06	22547,7
	0,17	0,12	0,07	0,093	-0,08	-0,13	-0,19	0,171657	-1,5E-06	-111202
	0,25	0,2	0,15	0,08	0,013	-0,05	-0,11	0,255342	1,72E-07
	0,3	0,25	0,2	0,13	0,05	-0,037	-0,06	0,309336	7,21E-07	428740,1
	0,36	0,31	0,26	0,19	0,11	0,06	-0,097	0,376403	-9,8E-06	-38392,7

Вычисляем П₅₊₁(0,263)=(0,263-x₀)(0,263-x₁)(0,263-x₂)(0,263-x₃)(0,263-x₄)

(0,263-x5)=0,1506492×10-6, сумма последнего столбца 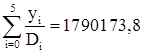, отсюда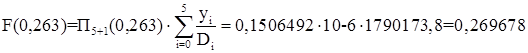

Вычисления вручную довольно громоздки и длительны, но такую таблицу легко составить с помощью электронной таблицы.

	A	B	C	D	E	F	G	H	I	J	K
	0,263
	i	xi	Разности	yi	Di	yi/Di
		0,05	=$A$1-$B3	=B3-$B$4	=B3-$B$5	=B3-$B$6	=B3-$B$7	=B3-$B$8	0,050042	=ПРОИЗВЕД (С3:H3)	=I3/J3
		0,1	=B4-$B$3						0,100335
		0,17							0,171657
		0,25							0,255342
		0,3							0,309336
		0,36							0,376403
									=ПРОИЗВЕД (С3,D4,E5, F6,G7,H8)		=СУММ (K3:K8)
									=I9*K9

Заполняем таблицу по образцу. Затем копируем ячейку C4 в C5:C8, ячейку D3 в D5:D8, ячейку E3 в E4, E6:E8, ячейку F3 в F4, F5, F7,F8, ячейку G3 в G4:G6, G8, ячейку H3 в H4:H7, ячейку C3 в D4, E5, F6, G7, H8, ячейку J3 в J4:J8, ячейку K3 в K4:K8.

В результате вычислений получаем в ячейке I10 значение многочлена Лагранжа.

Варианты самостоятельных работ для задачи 3 см. Приложение 2

Дата добавления: 2015-10-31