Метод Эйлера.

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод дает одновременно и способ нахождения искомой функции в табличной форме.

Пусть дано дифференциальное уравнение (6.1). Найти приближенное численное решение этого дифференциального уравнения, т.е. составить таблицу приближенных значений функции у=у(х) удовлетворяющей заданным начальным условиям.

x	x0	x1	x2	x3	x4	x5	…	xn
y	y0	y1	y2	y3	y4	y5	…	yn

Где, x_i=x₀+i×h, 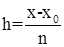– шаг таблицы.

Приближенно можно считать, что правая часть в (6.1) остается постоянной на каждом из отрезков между точками деления. Метод Эйлера состоит в непосредственной замене производной разностными отношениями по приближенной формуле:

y-y₀=f(x₀,y₀)×(x-x₀)

y=y₀+f(x₀,y₀)×(x-x₀)

если x=x₁, то

y₁=y₀+f(x₀,y₀)×(x₁-x₀)

y₁=y₀+h×f(x₀,y₀)

Dy₀=h×f(x₀,y₀)

если x=x₂, то

y₂₌y₁+f(x₁,y₁)×(x₂-x₁)

y₂=y₁+h×f(x₁,y₁)

Dy₁=h×f(x₁,y₁)

…

если x=x_i+1, то

y_i+1=y_i+h×f(x_i,y_i)

Dy_i=h×f(x_i,y_i)

Таким образом, получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом применении пары формул:

Dy_k=h×f(x_k,y_k)

y_k+1=y_k+Dy_k

где k=0, 1, 2, …,n

Геометрически эти формулы означают, что на отрезке [x_i, x_i+1] интегральная кривая заменяется отрезком касательной к кривой (см. рис. 6.3, рис. 6.4).

Пример 1

Решить методом Эйлера дифференциальное уравнение y'=cos y + 3 x с начальным условием y(0)=1,3 на отрезке [0, 1] приняв шаг h=0,2

k	xk	yk	Dyk=0,2×(cos yk+3×xk)
		1,3	0,05
	0,2	1,35	0,16
	0,4	1,52	0,25
	0,6	1,77	0,32
	0,8	2,09	0,38
		2,47

Алгоритм решения задачи на рис. 6.5.

Программу составить самостоятельно.

{Программа 6.1}

var x,y,a,b,h:real; {Метод Эйлера}

function f(x,y:real):real;

begin f:= cos(y)+3*x; end;

begin

writeln('введите y, a, b, h');

readln(y,a,b,h); x:=a;

repeat

writeln(x:0:3,' ',y:0:3);

y:=y+h*f(x,y);

x:=x+h;

until x>b+0.1;

readln; end.

Пример 2

Решить методом Эйлера дифференциальное уравнение y'=cos y + 3×x с начальным условием y(0)=1,3 на отрезке [0, 1] приняв шаг h=0,1

k	xk	y2k	yk
		1,3	1,30
	0,1		1,33
	0,2	1,35	1,38
	0,3		1,46
	0,4	1,52	1,56
	0,5		1,68
	0,6	1,77	1,82
	0,7		1,98
	0,8	2,09	2,15
	0,9		2,33
		2,47	2,53

Вывод: погрешность метода Эйлера слишком велика для решения практических задач. Дальнейшим развитием метода Эйлера явились методы Рунге-Кутта.

Дата добавления: 2015-10-31