Численные методы решения трансцендентных уравнений

Введение

Решение многих практических задач сводится к решению уравнений
f(x)=0 (5.1)

где функция f(x) определена и непрерывна на некотором интервале. Если функция f(x) представляет собой многочлен, то уравнение (5.1) называется алгебраическим; если же в функцию f(x) входят трансцендентные (тригонометрические, логарифмические, показательные и т.д.) функции, то уравнение (5.1) называется трансцендентным.

Алгебраические уравнения, которые рассматриваются в школе, решаются или аналитически (с помощью формул для уравнений не выше 4 степени), либо графически. Для решения алгебраических уравнений любой степени, трансцендентных уравнений разработаны численные методы. Решение уравнения (5.1) разбивается на 2 этапа:

1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2. вычисление выделенного корня с заданной точностью.

Для вычисления выделенного (изолированного) корня существует множество методов: метод половинного деления, метод итераций, метод Ньютона и т.д.

Пример 1.

Решить уравнение: cos x = 2x

Из рис. 5.1 видно, что наше уравнение имеет единственный корень, принадлежащий отрезку [0; 1]. Когда мы находим отрезок, внутри которого расположен корень, то этот этап решения называется этапом отделения корня.

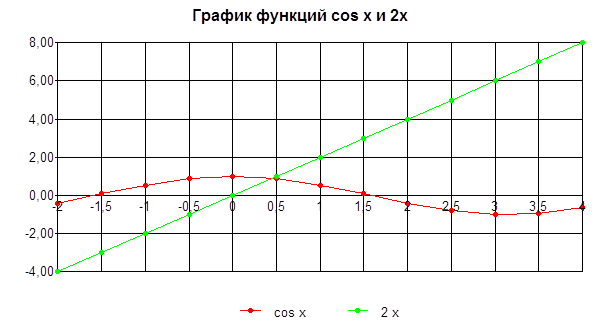
Рис. 5.1

Теорема

Рис 5.2

Если непрерывная функция f(x) на отрезке [a, b] строго монотонна и имеет на концах отрезка разные знаки, то на этом отрезке существует и причем единственный корень уравнения f(x)=0.

Действительно, функция f(x)=2x-cos x в точках x=0 и x=1 имеет разные знаки и возрастает на отрезке [0, 1]: f(0)=(2×0 - cos 0)=0-1=-1 <0; f(1)=(2×1 - cos 1)»2-(0,5)
»1,5 >0

Действительно, если f(a)<0 f(b)>0 (или наоборот), то непрерывная функция f(x) обязательно хотя бы 1 раз пересекает ось абсцисс (а иногда несколько раз, рис. 5.3).

Рис 5.3

Отделение корней осуществляют либо графически, либо на основании вышеприведенной теоремы, либо сочетают оба этих способа.

Для уточнения корней используют несколько различных методов (метод деления отрезка пополам, метод хорд, метод касательных). Рассмотрим метод деления отрезка пополам.

Дата добавления: 2015-10-31