Практическая работа на ЭВМ

1. Вызвать с диска программу korni1.pas и получить результаты решения системы уравнений:

а) б) в)

Ответы: а) x=1; y=1; б) x=4; y=5; в) x=5; y=3;

2. Составить программу для решения системы уравнений с тремя неизвестными по формулам Крамера и получить результаты для решения системы уравнений:

а) б)

Ответ: а) x=1; y=-2; z=-1; б) x=1; y=-3; z=-2

3. Вызвать с диска программу (gaus.pas) и получить результаты решения системы уравнений:

a) б)

Ответ: а) x=8; y=4; z=2; б) x=1; y=2; z=3

Домашнее задание.

I. Решить систему уравнений по формулам Крамера:

Ответ: x=1; y=2; z=1.

II. Решить систему уравнений по методу Гаусса:

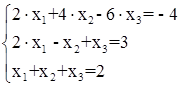Ответ: x₁=1; x₂=0; x₃=1.

III. Составить алгоритмы для решения систем линейных уравнений с двумя и тремя неизвестными.

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Постановка задачи

Задача интерполирования состоит в том, чтобы по значениям функции f(x) в некоторых точках отрезка восстановить ее значения в остальных точках отрезка.

Пример 1.

Известны некоторые значения функции – физической величины замеренные через 1 час. Необходимо найти значения в промежутках через 30 минут.

Пример 2.

Интерполирование применяется при сгущении таблиц, когда вычисление функции f(x) трудоемко и необходимо составить таблицу с меньшим шагом.

Пример 3.

Интерполирование применяется при необходимости приближенной замены функции другими функциями, которые легче вычислить. Например, когда вычисляется определенный интеграл некоторой неинтегрируемой функции, такая функция заменяется многочленом, аналогично при вычислении производных и т.д.

Пусть дана функция y=f(x) для которой известна лишь таблица ее значений: (*)

x	x0	x1	x2	x3	…	xn
y	y0	y1	y2	y3	…	yn

При этом требуется получить значение функции y=f(x) для такого значения аргумента х, которое входит в отрезок [x₀, x_n], но не совпадает ни с одним из значений x_i, i=0, 1, 2,…,n, т.е. xÎ[x₀, x_n], x¹x_i, i=0, 1, 2,…,n.

Очевидный прием решения этой задачи – вычислить значение функции f(x) воспользовавшись аналитическим выражением функции f. Однако это можно применить, если аналитическое выражение функции f известно и пригодно для вычисления. Но часто аналитическое выражение функции f вовсе неизвестно.

В этом случае используется особый прием – построение по исходной таблице приближающей функции F, которая в некотором смысле близка к функции f, и аналитическим выражением которой можно воспользоваться для вычислений, считая приближенно, что f(x)=F(x)

Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках x_i, i=0, 1, 2,…,n.

F(x₀)=f(x₀)=y₀;

F(x₁)=f(x₁)=y₁;

… (3.1)

F(x_n)=f(x_n)=y_n.

Второе требование для функции F: функция F должна быть многочленом степени n (степень на единицу меньше числа точек). В этом случае нахождение приближающей функции называют интерполяцией.

Определение. Интерполяция – нахождение приближающей функции. Функция F называется интерполирующей, точки x₀, x₁, x₂, …, x_n – узлы интерполяции.

Будем искать функцию F в виде многочлена степени n:

F(x)=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n

Зная условие (3.1) можно найти коэффициенты a_i, i=0, 1,…, n. Получаем систему из n+1 уравнения с n+1 неизвестными.

Эта система имеет единственное решение, т.к. по нашему предположению все x_i различны. Решая эту систему относительно неизвестных a₀, a₁, …, a_n мы получим аналитическое выражение многочлена.

Описанный прием можно использовать при решении задач интерполирования, но на практике используют другие более удобные и менее трудоемкие методы.

Дата добавления: 2015-10-31