
|
Читайте также: |
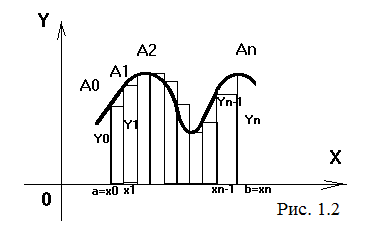 |
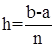 . Точки деления будут: x0=a; x1=a+h; x2=a+2×h,..., xn-1=a+(n-1)×h; xn=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y0, y1, y2,..., yn. Cтало быть, y0=f(a), y1=f(x1), y2=f(x2),..., yn=f(b). Числа y0, y1, y2,..., yn являются ординатами точек графика функции, соответствующих абсциссам x0, x1, x2,..., xn (рис. 1.2). Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.
. Точки деления будут: x0=a; x1=a+h; x2=a+2×h,..., xn-1=a+(n-1)×h; xn=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y0, y1, y2,..., yn. Cтало быть, y0=f(a), y1=f(x1), y2=f(x2),..., yn=f(b). Числа y0, y1, y2,..., yn являются ординатами точек графика функции, соответствующих абсциссам x0, x1, x2,..., xn (рис. 1.2). Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.
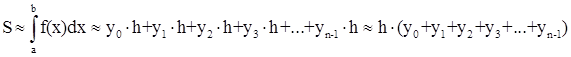 (1.3)
(1.3)
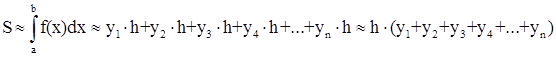 (1.4)
(1.4)
Формула (1.3) называется формулой левых прямоугольников, (1.4) - формулой правых прямоугольников, (1.5) - формулой средних прямоугольников.
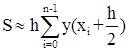 (1.5)
(1.5)
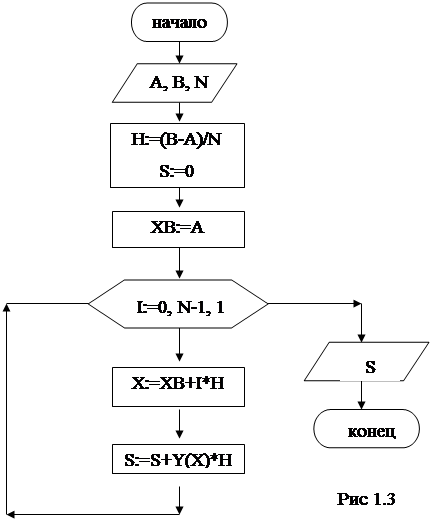
Алгоритм вычисления для формулы (1.3)
 |
Задача 1.
Вычислить по методу левых прямоугольников: 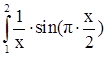
{Программа 1.1}
program integral1;{Метод левых прямоугольников}
uses crt;
var i,n:integer; a,b,h,x,xb,s:real;
function f(x:real):real;
begin f:=(1/x)*sin(3.14*x/2); end;
begin
clrscr;
gotoxy(10,10);
textbackground(1);
write('Введите нижний предел интегрирования ');
readln(a);
gotoxy(10,12);
write('Введите верхний предел интегрирования ');
readln(b);
gotoxy(10,14);
write('Введите количество отрезков ');
readln(n);
h:=(b-a)/n; s:=0; xb:=a;
for i:=0 to n-1 do
begin x:=xb+i*h; s:=s+f(x)*h; end;
gotoxy(10,18);
writeln('Интеграл равен ',s:12:10); readln;
end.
Задача 2
Вычислить по методу правых прямоугольников: 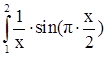
{Программа 1.2}
program integral; {Метод правых прямоугольников}
uses crt;
var i,n:integer; a,b,h,x,xb,s:real;
function f(x:real):real;
begin f:=(1/x)*sin(3.14*x/2); end;
begin
clrscr; gotoxy(10,10); textbackground(1);
write('Введите нижний предел интегрирования ');
readln(a); gotoxy(10,12);
write('Введите верхний предел интегрирования ');
readln(b); gotoxy(10,14);
write('Введите количество отрезков '); readln(n);
h:=(b-a)/n; s:=0; xb:=a;
for i:=1 to n do
begin x:=xb+i*h; s:=s+f(x)*h; end;
gotoxy(10,18);
writeln('Интеграл равен ',s:12:10); readln;
end.
Задача 3
Вычислить по методу средних прямоугольников: 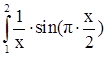
{Программа 1.3}
program integral; {Метод средних прямоугольников}
uses crt;
var i, n: integer; a, b, dx, x, s, xb: real;
function f(x: real):real;
begin f:=(1/x)*sin(3.14*x/2); end;
begin
clrscr; gotoxy(10,10); textbackground(1);
write('Введите нижний предел интегрирования ');
readln(a); gotoxy(10,12);
write('Введите верхний предел интегрирования ');
readln(b); gotoxy(10,14);
write('Введите количество отрезков '); readln(n);
dx:=(b-a)/n; xb:=a+dx/2;
for i:=0 to n-1 do
begin x:=xb+i*dx; s:=s+f(x)*dx; end;
gotoxy(10,18);
write('Интеграл равен ',s:15:10); readln;
end.
Дата добавления: 2015-10-31; просмотров: 154 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ | | | Практическая работа на ЭВМ |