Практическая работа на ЭВМ. 1. Вызвать с диска программу 1.1 (метод левых прямоугольников): файл int1.pas

1. Вызвать с диска программу 1.1 (метод левых прямоугольников): файл int1.pas

2. Внести изменения в программу, заменив функцию 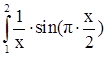на функцию согласно своему варианту (Приложение 1). Получить результаты для:
n=10; 20; 100.

3. Вычислить интеграл по формуле правых прямоугольников (Программа 1.2). Получить результаты для n=10; n=20; n=100.

4. Вычислить интеграл по формуле средних прямоугольников (Программа 1.3). Получить результаты для: n=10; n=20; n=100.

5. Вызвать с диска программу 1.4 (метод трапеций): файл int4.pas

6. Внести изменения в программу, заменив функцию 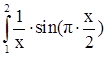на функцию согласно своему варианту. Получить результаты для: n=10; 20; 100.

7. Вызвать с диска программу 1.5 (метод Симпсона): файл int5.pas.

8. Внести изменения в программу, заменив функцию 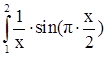на функцию согласно своему варианту. Получить результаты для: n=10; 20; 100.

9. Сделать вывод о численных методах вычисления определенного интеграла.

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

О системах линейных уравнений.

Многие задачи практики приводят к необходимости решать системы линейных уравнений. При конструировании инженерных сооружений, обработке результатов измерений, решении задач планирования производственного процесса и ряда других задач техники, экономики, научного эксперимента приходится решать системы линейных уравнений.

Решение систем линейных уравнений с двумя неизвестными по формулам Крамера.

Пусть дана система линейных уравнений с двумя неизвестными:

(2.1)

Рассмотрим решение систем линейных уравнений с двумя и тремя неизвестными по формулам Крамера.

Теорема 1. Если главный определитель системы отличен от нуля, то система имеет решение, притом единственное. Решение системы определяется формулами: 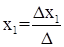, (2.2)

где x₁, x₂ - корни системы уравнений, D – главный определитель системы, Dx₁, Dx₂ - вспомогательные определители.

Главный определитель системы определяется:

Вспомогательные определители:

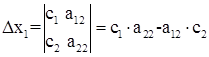
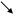
Пример 1.

Решить систему уравнений по формулам Крамера:

Решение:

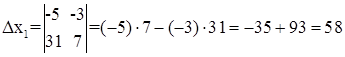
Ответ: x₁=2; x₂=3

{Программа 2.1}

program korni1; {Метод Крамера для системы }

label Out; {уравнений с двумя неизвестными}

var a: array[1..2,1..3] of integer;

x,y,dx,dy,d:real; i,j:integer;

begin

for i:=1 to 2 do

for j:=1 to 3 do readln(a[i,j]);

d:=a[1,1]*a[2,2]-a[2,1]*a[1,2];

if d=0 then begin

writeln('Единственого решения нет'); goto Out; end;

dx:=a[1,3]*a[2,2]-a[2,3]*a[1,2];

dy:=a[1,1]*a[2,3]-a[2,1]*a[1,3];

x:=dx/d; y:=dy/d;

writeln('x=',x); writeln('y=',y);

Out: end.

Дата добавления: 2015-10-31