Решение систем линейных уравнений способом Гаусса.

Метод Гаусса для практических вычислений значительно удобнее, чем формулы Крамера. Казалось бы, формулы Крамера дают возможность легко вычислить значения неизвестных и получить решение системы. В принципе это так, но на практике дело осложняется тем, что для отыскания решения системы по формулам Крамера требуется выполнить чрезмерно много вычислений. Установлено, что для отыскания решения системы n уравнений по формулам Крамера требуется произвести N=(n²-1)×n!+n одних только умножений и делений. Приведем таблицу, указывающую число арифметических действий при решении систем по формулам Крамера и способом Гаусса.

n	в случае применения формулы Крамера	в случае применения способа Гаусса
	360×10^6
	76×10^66

Метод Гаусса (метод последовательного исключения неизвестных) имеет много разных вычислительных схем. Рассмотрим схему единственного деления. Суть метода Гаусса состоит в следующем.

Пусть дана система линейных уравнений с тремя неизвестными:

(2.5)

Система путем последовательного исключения неизвестных приводится к системе с треугольной матрицей, из которой затем определяются значения неизвестных. Рассмотрим процесс исключения неизвестных. Пусть a₁₁<>0. Разделим первое уравнение на a₁₁ . Затем из каждого i-го (i>=2) уравнения вычтем полученное после деления первое, умноженное на a_i1. Получим систему:

(2.6)

где (2.7)

В результате этих преобразований неизвестное x₁ оказалось исключенным из всех уравнений, кроме первого. Рассмотрим теперь систему (2.6). Пусть . Разделим второе уравнение на . Затем из каждого i-го (i ³ 3) уравнения вычтем полученное второе, умноженное на . Получим систему, в которой неизвестное x₂, будет исключено из всех уравнений, кроме 1-го и 2-го. Продолжая аналогичным образом процесс, в итоге получим систему вида:

(2.8)

Коэффициенты системы (2.8) можно представить в виде треугольной матрицы с единичной главной диагональю. Из системы (2.8) легко определяются значения неизвестных. Из последнего уравнения сразу определяется x₃. Подставляя x₃ в предпоследнее уравнение, находим x₂. Аналогично находим x₁. Приведение системы (2.5) к виду (2.8) называется прямым ходом метода Гаусса. Определение значений неизвестных из системы (2.8) называется обратным ходом метода Гаусса. Если на каком-то шаге на главной диагонали окажется нулевой элемент, то необходимо произвести перестановку строк.

Пример 3. Решить систему уравнений по методу Гаусса.

Решение.

1. Уравнение (1) разделим на a₁₁, т.е. на 2, получим уравнение 4.

2. Умножим полученное уравнение (4) на a₂₁, т.е. на 1, получим уравнение (5).

3. Вычтем из уравнений (2) и (3) уравнение (5), получим уравнения (6) и (7).

6. Уравнение (6) разделим на a₂₂, т.е. на 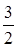, получим уравнение (8).

7. Умножим уравнение (8) на a₃₂, т.е. на , получим уравнение (9).

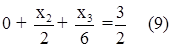
8. Вычтем из уравнения (7) уравнение (9) получим уравнение (10).

9. Итак, прямой ход закончен, начинаем обратный ход. Подставим (10) в уравнение (8), получим x₂=2 (11)

10. Подставим (11) и (10) в уравнение (5), получим: x₁=1 (12)

Ответ: x₁=1; x₂=2; x₃=3

{Программа 2.3}

program GAUS; {Метод Гаусса для системы }

{уравнений с тремя неизвестными}

VAR A:array[1..3,1..3] of real;

D,B,X:ARRAY[1..3] OF REAL;

m,s:real; i,j,k:integer;

begin

for i:=1 to 3 do

for j:=1 to 3 do read(a[i,j]);

readln;

for i:=1 to 3 do readln(b[i]);

{Исключение неизвестных}

for k:=1 to 2 do

for i:=k+1 to 3 do

begin

m:=a[i,k]/a[k,k];

for j:=k+1 to 3 do

a[i,j]:=a[i,j]-m*a[k,j]; b[i]:=b[i]-m*b[k];

end;

{Обратная подстановка}

x[3]:=b[3]/a[3,3];

for i:=2 downto 1 do

begin

s:=0;

for j:=i+1 to 3 do s:=s+a[i,j]*x[j];

x[i]:=(b[i]-s)/a[i,i];

end;

for i:=1 to 3 do

writeln('x',i,'=',x[i]);

end.

Дата добавления: 2015-10-31