Несколько определений

Приведенные примеры показывают, что решение задач на нахождение функции по заданным свойствам, сводится к решению уравнения, связывающего искомую функцию и величины задающие её свойства. Поскольку свойства функции выражаются через её производные, то решая указанную выше задачу мы приходим к уравнению связывающему искомую функцию и её производные. Такие уравнения называются дифференциальными. Решая полученное дифференциальное уравнение находят искомую функцию.

Определение. Дифференциальным уравнением называется уравнение, связывающее аргумент, функцию этого аргумента и производные этой функции до некоторого порядка включительно.

Определение. Наивысший порядок производной входящей в дифференциальное уравнение называется порядком уравнения.

Какого порядка уравнения в примерах 1, 2, 3?

Определение. Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество. График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Пример 1

Покажем, что функция y=x является решением дифференциального уравнения для всех х¹0

y'=1 Þ – справедливо для всех х¹0

Простейшим дифференциальным уравнением является уравнение y'=f(x). y=òf(x)dx – решение этого уравнения. Если F(x) её первообразная, то y=F(x)+C. Таким образом это уравнение имеет бесконечное множество решений и их графики получаются параллельным переносом в направлении оси ординат. При этом через каждую точку M(x₀, y₀), такую что функция f непрерывна при х=х₀, проходит только одна кривая. В примере 1 функция у=С×х является решением дифференциального уравнения.

Определение. Функцию y=j(x,C), где С – произвольная постоянная, называют общим решением дифференциального уравнения y'=f(x,y) в области G, если
а) для любого С она является решением этого уравнения, т.е. j'(x, C)=f(x,j(x, C))
б) для любой точки M(x₀,y₀) из области G, существует единственное значение С₀ при котором линия y=j(x,C₀) проходит через точку M₀, т.е. y₀=j(x₀,C₀)

Таким образом у=С×х – общее решение уравнения 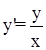, для всех х¹0

Определение. Решение дифференциального уравнения, получаемое из общего решения путем придания определенного значения произвольной постоянной, называют частным решением этого уравнения.

Обычно при отыскании частного решения дифференциального уравнения указывается значение искомой функции у₀ в некоторой фиксированной точке х₀.

Таким образом, равенство у(х₀)=у₀ определяет так называемые начальные условия. Зная общее решение дифференциального уравнения и имея начальное условие, подставляют их в общее решение и находят соответствующее значение параметра С, выделяющее искомое частное решение из общего решения.

Пример 2

Найти частное решение уравнения , удовлетворяющее начальному условию у(1)=2

Решение:

Общее решение: у=С×х. Полагая у₀=2, х₀=1 получим 2=С×1 и Þ С=2

Частное решение: у=2х

Дата добавления: 2015-10-31