
Читайте также:
|


Оценка погрешности формулы Лагранжа
Rn(x)= f(x) - Ln(x)
Rn(xi) =0 i=0..n
будем изучать что на [a;b] фнк имеет до n+1 производные
введем ψ(x) = f(x) - Ln(x) - k Πn+1(x) (10) //k=? = const
ψ(x) имеет n+1 корень
подберем  так чтобы ψ(
так чтобы ψ( ) =0,
) =0, 
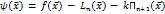 ,
,  !=0
!=0
 (11)
(11)

Правило Ролля (Тролля))
найдется такая точка Ы что  тогда на концах [Ыi, Ыi+1] найдется такая формула
тогда на концах [Ыi, Ыi+1] найдется такая формула 
 =
=  (12) =>
(12) =>
 (13)
(13)
если сравнить (11) и (13) то  ,
,


Оценка погрешности формулы ньютона

q = (x-x0)/h;
I:  (16)
(16)
II:  (17)
(17)
I: 

II: 

что такое Ы смотри предыдущий билет
заведем некое 
I: 

II:  (21)
(21)
I: 

II:  (23)
(23)

I: 

II: 

Интерполяция сплайнами


Тотчетное среднеквадратичное приближение функций

Интегральное среднеквадратичное приближение функций

Численное интегрирование. формула Ньютона-Котеса
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых x = a и x = b, где a и b — пределы интегрирования
(1) 
Методы приближенного интегрирования интеграла (1) приходится применять, если:
· (1) не берется в элементарных функциях
· Громоздкая первообразная
· Подынтегральная фнк задана таблично
Приближенные формулы = квадратурные.
Формула Ньютона-Котеса.
 -шаг
-шаг




[a,b] делим на n равных частей

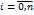
 заменяем соответствующим полиномом Лагранжа (R - погрешность)
заменяем соответствующим полиномом Лагранжа (R - погрешность)
(2) 

 - узлы кв. ф-лы;
- узлы кв. ф-лы;  – коэффициенты пост. квадратурной формулы;
– коэффициенты пост. квадратурной формулы;  ,
,  -не зависят от
-не зависят от 






Значит 




(a<=x<=b) (5)=> (0<=q<=n)




(3) будет иметь вид:

· n=0 -> формула прямоугольников
· n=1 -> формула трапеций
·  n=2 -> формула Симпсона
n=2 -> формула Симпсона
· n>2 -> формула Ньютона-Котеса высших порядков
Формула трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
| X1 |
| y1 |
| y0 |
| X0 |




Оценим погрешность R



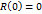
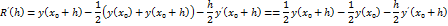


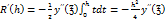

По теор. О среднем:





Параметры в формуле трапеции дважды дифференцируемы пропорц. 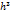
При малом h этой погрешностью можно пренебречь.
Дата добавления: 2015-10-26; просмотров: 285 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Данилевского | | | Проверка на прочность. |