Предмет и метод вычислительной математики

Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач.

Выч Эксперимент (ВЭ) - исследование, реализация процессов средствами ВычМата

5 этапов ВЭ:

1) мат формулировка задачи(выбор мат модели)

а) проверяется правильность входных данных

б) проверяется, имеет ли задача вообще решение

в) единственное ли решение имеет задача (если их несколько ото отделить решения)

г) проверить, не имеет ли задача аналитического решения, или частные случаи где задача имеет решение

2) построение приближенного метода решения задачи и написание вычислительного алгоритма

выч. алгоритм - последовательность арифм.и лог. операций, с помощью которых находится решение задачи

3) программирование:

если алгоритм пишем сами:

а) отладка

б) оптимизация

в определенных случаях можно юзать спец проги wolfram mathematic mathCad

4) проведение расчетов

а) тестирование

б) проведение серии расчетов

5) анализ полученных результатов и уточнение полученной модели

Структура погрешности

4 источника погрешности:

- мат модель

- исходные данные

- метод - приближенный

- погрешность округления

погрешность исходных данных приводит к неустранимой погрешности.

появляется при измерениях приборами

Ax = y

А - оператор

х - класс исходных данных

у - класс искомых данных

оператор А заменяется приближенным _А

_А - приближенное значение оператора А

_х=х+∆х - с погрешностью: _А_х=_у

погрешность метода дб в 2-5 раз меньше погрешности исходных данных

погрешности округления:

- абсолютная погрешность

- относительная погрешность

Корректность:

задача называется Корректно поставленной если для 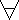входных данных Х из класса решения У:

-

- !

- устойчиво по вх данным

погрешность:

у + 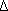у = А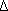(х+ х)

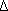у = А(х+ 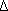х) - Ах

Если решение непрерывно зависит от вх данных т.е. всегда:

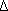|| y||->0 при || 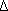x|| ->0 то решение устойчиво по вх данным иначе задача не устойчива по входным данным

(русский вариант: если малое изменение 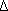х сильно влияет на 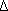у то не устойчива)

y=Ax -> - называется корректным если существует и единственное приближение решения для любых входных данных х и оно устойчиво относительно всех ошибок в исходных данных и промежуточных выкладках

Дата добавления: 2015-10-26