Метод итерации. для решения СЛАУ. Оценка погрешности

-?

выберем некоторое натуральное р>0

если многократно воспользоваться тем что для сходимости ||a||<=1 то

при р->inf =>

(8)

(9)

(10)

Доп инфа:

если 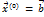то ,

(11)

оценка погрешности позволит узнать количество операций

k -? , решить относительно k

Метод Зейделя.

Метод Зейделя представляет собой некоторую модификацию метода итерации. Основная его идея заключается в том, что при вычислении -ого приближения неизвестной учитываются уже вычисленные ранее -ые приближения неизвестных , ,..., .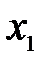

Пусть дана приведенная линейная система 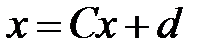. Выберем произвольно начальное приближение , ,…, . Далее предполагая что k -ое приближение известно, вычисляем -ое приближение по формулам

,

,

………………………………..

,

…………………….

.

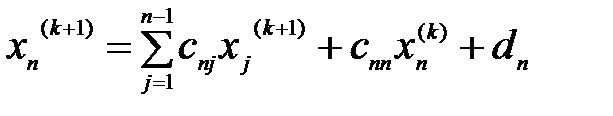Заметим, что для сходимости метода Зейделя достаточно, чтобы выполнялось условие 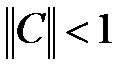для какой-либо нормы матрицы. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации.

Метод половинного деления

Метод хорд

10. Метод Ньютона (касательных)

Метод секущих

применяется если f(x) мало меняется на [a;b]

Комбинированный метод

Требуется найти все или несколько корней уравнения:

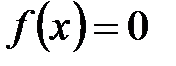(1)

Пусть и - приближенные значения корня по недостатку и по избытку. 2 последовательности по методам касательных и хорд

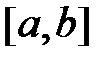а) Если на , то

,

при этом .

б) Если 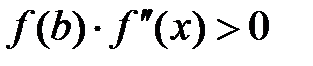на , то

,

при этом .

метод работает пока на выполнится условие

где - точность

13. Метод итераций для решения трансцендентных уравнений. Сходимость

Метод итераций для решения трансцендентных уравнений. Оценка погрешности

Достаточное условие сходимости метода итераций:

пусть определена и непрерывно дифференцируема на [a;b]

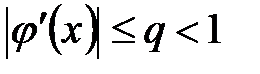и то существует q: 0<q<1: то процесс итераций сходится и существует 1 корень ур-я (2) => и ур-я (1) вне зависимости от выбора начального приближения

(11)

(12)

решаем относительно n и узнаем при каком n (12) будет , ибо считается что должно быть

Дата добавления: 2015-10-26