Метод Данилевского

До определения коэффициентов характеристического уравнения матрицу A/* A= matrix[n](a_ij)*/ с помощью n-1 преобразований подобия заменяют подобной ей матрицей Фробениуса

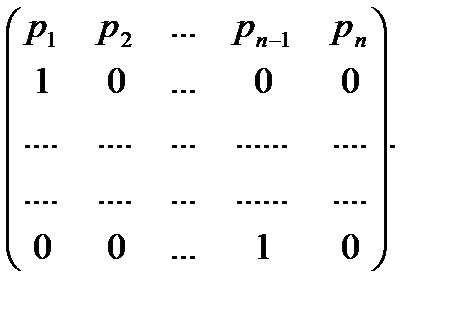= P

где p_i- коэффициенты ее характеристического многочлена

S: P = S^-1AS

На первом этапе делаю следующее:

(a_n1,a_n2,..,a_nn) -> (0,0,...,1,0), при условии что a_nn-1!=0

потом все эл-ты n-1 столбца делим на a_nn-1 (a_n1,a_n2,..,1,a_nn) и теперь из каждого столбца вычитают n-1й умноженный на a_nj т.е.

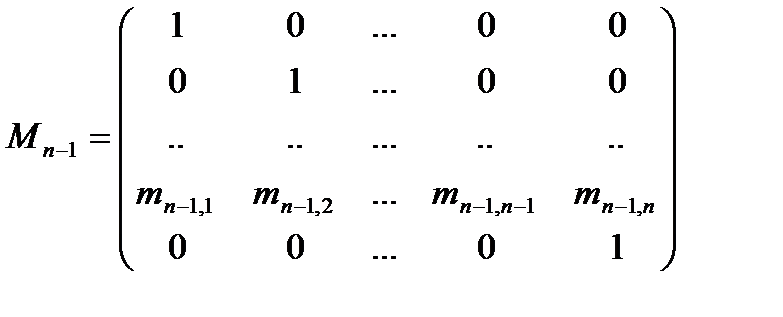
где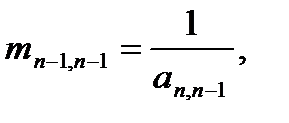

B=AM_n-1

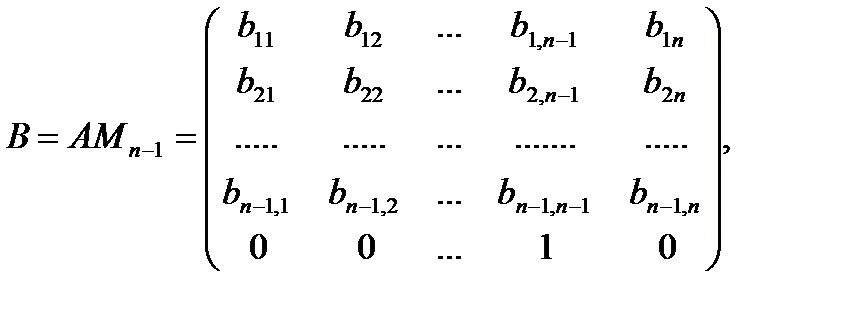
где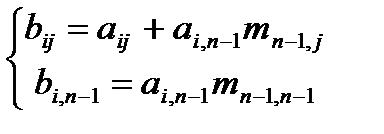

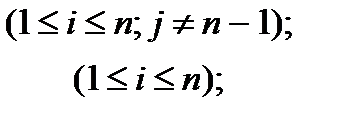
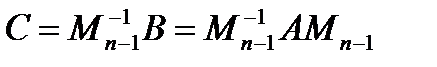(матрица С подобна матрице А);

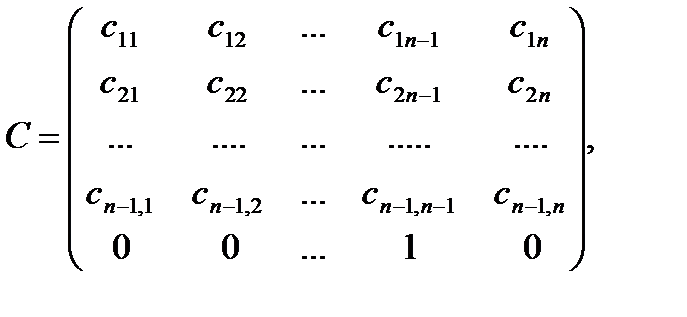
где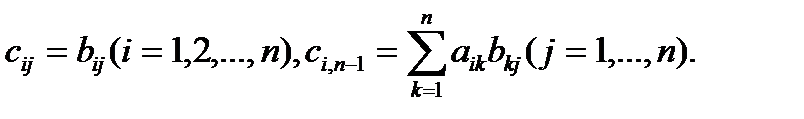

Шаг 2:

Матрицу С преобразуем в D Теперь повторяем все вышесказанные для n-2 столбца и так далее n-1 раз и получим форму Фробениуса

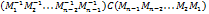
теперь находим :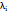

- аналитически

- метод хорд\касательных и т.д

- Лобачевского

Вычисление собственных векторов по методу Данилевского

λ - собственные значения которые уже известны

дано λ,А,Р

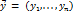- собственный вектор P(см 18й билет)

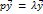
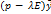= 0

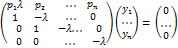
получим

...

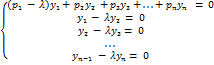
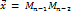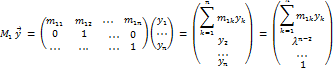
Нахождение наибольшего по модулю собственного значения матрицы и соответствующего собственного вектора

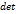(A - λE) =0

- собственные вектора

Определение Первым собственным значением 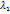называется наибольшее по модулю собственное значение матрицы А

нахождение 1ого СЗ является частной проблемой собственных значений

пусть у А ∃! собственное значение тогда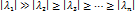

Теорема Перрона

если А - действително(е,я?????) и все эл-ты А >0 то 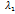- действительное число

Итерационный метод нахождения 1ого СЗ

возьмем произвольный вектор и разложим по собственному вектору

(1)

A - итерация вектора

а считать мы будем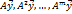

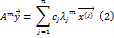
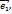..., . разложим N-ую итерацию по этому базису

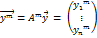, m =1,2,3....

/* */

Собственный вектор разложим по базису

(3) подставим в (2)

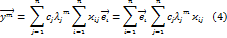
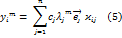
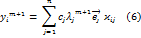
будем полагать что с₁!=0 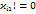- этого всегда можно добиться

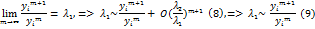
Вывод:

1) берем произв. вектор 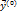(m=0)

2) вычисляем m+1-ию итерацию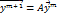

3) находим N-ое приближение 1ого СЗ

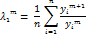
4) находим (n+1)ое приближение

5) сравниваем

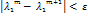
если условие выполняется то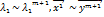

если нет то в пункт 6

6) нормируем вектор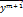

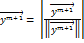
Интерполирование функцией

Конечные разности и их свойства

Первая интерполяционная формула ньютона

Вторая интерполяционная формула ньютона

Дата добавления: 2015-10-26