Лекция 9. Численное интегрирование и дифференцирование.

Ставится задана вычислить интеграл вида

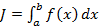(9.1)

где а и b - нижний и верхний пределы интегрирования; f(x) – непрерывная функция на отрезке [а, b].

К численному интегрированию обращаются тогда, когда нельзя через элементарные функции аналитически записать первообразную интеграла (9.1) или когда подобная запись имеет сложный вид.

Сущность большинства методов вычисления определенных интегралов состоит в замене подынтегральной функции f(x) аппроксимирующей функцией φ(x), для которой можно легко записать первообразную в элементарных функциях, т.е.

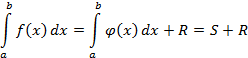
где S - приближенное значение интеграла; R - погрешность вычисления интеграла

Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции. Дадим краткую характеристику групп наиболее распространенных методов.

Методы Ньютона-Котеса основаны на полиномиальной аппроксимации подынтегральной функции. Методы этого класса отличаются друг от друга степенью используемого полинома, от которой зависит количество узлов, где необходимо вычислить функцию f(x). Алгоритмы методов просты и легко поддаются программной реализации.

Сплайновые методы базируются на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочный полином. Методы различаются по типу выбранных сплайнов. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются для обработки данных.

В методах наивысшей алгебраической точности (методы Гаусса-Кристоффеля и другие) используются неравноотстоящие узлы, расположенные по алгоритму, обеспечивающему минимальную погрешность интегрирования для наиболее сложных функций при заданном количестве узлов. Методы различаются способами выбора узлов и широко используются для интегрирования, в том числе они применимы и для несобственных интегралов. Хотя из-за необходимости хранения числовых констант и стандартизации пределов интегрирования программы указанных методов требуют несколько большего объема памяти по сравнению с методами Ньютона-Котеса.

В класс специальных группируются методы, алгоритмы которых разрабатываются на основе учета особенностей конкретных подынтегральных функций, что позволяет существенно сократить время и уменьшить погрешность вычисления интегралов.

Дата добавления: 2015-10-29