Б) Розмірність і базис

Вектори а₁, а₂, …, а_k векторного простору V називаються лінійно залежними, якщо існують такі числа одночасно не рівні нулю, що

В іншому випадку вектори називають лінійно незалежними.

Максимальна кількість лінійно незалежних векторів системи векторів а₁, а₂, …, а_k називається рангом цієї системи. Позначають rank{ а₁, а₂, …, а_k }.

Ранг системи рядків довільної матриці А дорівнює рангу її стовпчиків і називається рангом матриці А. Позначається rankA або r(A).

Розмірністю векторного простору V називається максимальна кількість лінійно незалежних векторів, що містяться в ньому. Позначається dimV

(від dimage -фр).

Наприклад, розмірність множини всіх векторів площини дорівнює два, розмірність множини просторових векторів – три. Простори із скінченною розмірністю називаються скінченновимірними.

Базисом простору V називають впорядковану скінченну систему векторів, якщо:

1) вона лінійно незалежна;

2) кожний вектор простору V є лінійною комбінацією векторів цієї системи.

Коефіцієнти даної лінійної комбінації називаються компонентами або координатами вектора за цим базисом.

Матриця А називається матрицею переходу від базису е до базису 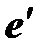. Матриця переходу є невиродженою, оскільки в іншому випадку її стовпчики, а, отже, і вектори 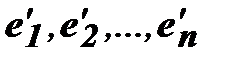, були б лінійно залежними.

В) Підпростори векторного простору

Підпростором векторного простору V називається сукупність V₁ його елементів, яка сама є векторним простором відносно введених в V операцій додавання і множення на число.

Перетином двох підпросторів V₁ і V₂ векторного простору V називається множина всеможливих векторів із V, що належить одночасно і V₁, і V₂. Перетин теж є підпростором і позначається

Сумою двох підпросторів V₁ і V₂ називається множина векторів вигляду де Сума теж є підпростором і позначається V₁ + V₂.

Теорема. Якщо V₁ і V₂ – підпростори векторного простору V, то

Дата добавления: 2015-10-29