Нормальна форма Жордана

В алгебраїчно замкненому полі, в тому числі і комплексному просторі, канонічним виглядом довільної матриці є так звана жорданова нормальна форма матриці. Розглянемо її.

Жордановою кліткою називається квадратна матриця вигляду

,

в якій на головній діагоналі знаходиться одне і те ж число 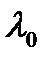, над головною діагоналлю – всюди число , а всі решта елементи – нулі.

ного вигляду (не існує власного базису).

Жордановою матрицею називається матриця вигляду

,

де – жорданові клітки деяких (не обов’язково різних) порядків, всі інші клітки заповнені нулями. Числа є власними значеннями перетворення 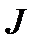з матрицею .

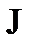Квадратні матриці порядку , елементами яких є многочлени довільних степенів від однієї невідомої 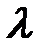з коефіцієнтами із поля Р, називаються многочленними матрицями або 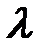-матрицями.

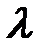-матриці А(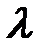)та В(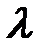) називаються еквівалентними, якщо від матриці А(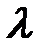) до матриці В(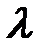) можна перейти шляхом скінченої кількості елементарних перетворень.

Канонічною 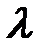-матрицею називається 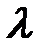-матриця, яка володіє властивостями:

1) ця матриця є діагональною, тобто має вигляд ;

2) всякий многочлен е_і(λ) націло ділиться на многочлен е_і-1(λ);

3) кожний многочлен е_і(λ) є зведеним.

Теорема 1. Будь-яка 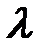-матрицяз допомогою елементарних перетворень зводиться до канонічного вигляду, причому однозначно.

(4).

Ми отримали спосіб безпосереднього знаходження многочленів е_k(λ), які називаються інваріантними множниками матриці А().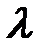

Мінімальним многочленом матриці називається зведений незвідний многочлен, для якого ця матриця є коренем.

Теорема 2. Якщо многочлени із кільця – попарно взаємно прості, то має місце така еквівалентність:

~ .

Із означення подібності матриць і з побудови канонічного вигляду характеристичної до жорданової матриці випливає очевидний висновок: дві жорданові матриці подібні тоді і тільки тоді, якщо вони складаються із одних і тих же жорданових кліток (тобто відрізняються тільки розміщенням цих кліток вздовж головної діагоналі).

Із цього твердження випливає:

1) жорданова нормальна форма визначається для матриці однозначно (з точністю до розміщення жорданових кліток вздовж головної діагоналі);

2) жорданова матриця, подібна до діагональної матриці, сама діагональна;

3) дві діагональні матриці подібні тоді і тільки тоді, якщо вони отримуються одна з одної перестановкою чисел, які знаходяться на головній діагоналі.

Необхідна і достатня умова зведення матриць до жорданової нормальної форми

Теорема 3. Кожна квадратна матриця порядку з елементами з поля 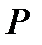зводиться в полі до жорданової нормальної форми тоді і тільки тоді, якщо всі характеристичні корені матриці знаходяться в полі .

Необхідна і достатня умова зведення матриць до діагонального вигляду

На основі отриманих результатів може бути сформульована, нарешті, необхідна і достатня умова звідності матриць до діагонального вигляду.

Теорема 4. Матриця порядку з елементами з поля 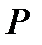зводиться до діагональ-ного вигляду тоді і тільки тоді, якщо усі її характеристичні корені (або всі корені останнього інваріантного множника її характеристичної матриці) знаходяться в полі , причому серед цих коренів немає кратних.

Дата добавления: 2015-10-29