В) Ортогональні перетворення

Лінійне перетворення A евклідового простору V називається ортогональним, якщо воно зберігає скалярний добуток векторів, тобто якщо x, y 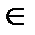V (A x, A y) = (x, y).

Це означає, що ортогональне перетворення зберігає довжини векторів та кути між ними (тому ортогональні перетворення іноді називають ізометричними).

Ясно, що ортогональне перетворення переводить довільний ортонормований базис в ортонормований і навпаки.

Властивості:

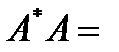
1. , тобто .

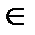Дійсно, якщо A - ортогональне перетворення і - спряжене до нього перетворення, то x, y V

(x, y) = (A x, A y) = (x, A ^*(A y)) = (x, A ^* A y).

Значить, або . Із отриманих рівностей видно, що ортогональне перетворення завжди не вироджене.

2. Перетворення обернене до ортогонального, теж ортогональне.

Дійсно, якщо , то .

Сума ортогональних перетворень, взагалі кажучи, не буде ортогональним перетворенням.

3. Добуток ортогональних перетворень є ортогональним перетворенням.

Дійсно, .

Матриця A, для якої A' = A^{- 1}, називається ортогональною матрицею.

4. Визначник ортогональної матриці дорівнює .

Дійсно, із AA' = E випливає: | AA' | = | A || A' | = | E | = 1.

Оскільки | A | = | A' | (транспонування не змінює визначника), то:

| A |² = 1, і .

5. Власні значення ортогонального перетворення дорівнюють .

Дійсно, якщо x - власний вектор і - відповідне йому власне значення ортогонального перетворення A, то:

(x, x) = (A x, A x) = (λ x, λ x) = λ²(x, x),

звідки, оскільки (x, x) ≠ 0, отримуємо , і .

6. Якщо підпростір інваріантний відносно ортогонального перетворення A, то його ортогональне доповнення теж інваріантне відносно A.

10.Білінійні і квадратичні функції(форми)

Лінійна функція (форма)

Кажуть, що в векторному просторі V задана лінійна функція f (x), якщо кожному вектору x 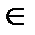V поставлено у відповідність число f (x), так, що виконані наступні умови:

1. f (x + y) = f (x) + f (y),

2. f (α x) = α f (x),

де х, у – довільні вектори із V, а α - будь-яке дійсне число.

Поняття білінійної та квадратичної функції

Задана у векторному просторі V функція двох змінних А (х, у) називається білінійною, якщо при фіксованому х вона лінійна за змінною у, а при фіксованому у – лінійна за х.

Отже, якщо А (х, у) - білінійна функція, то при всіх x, y, z 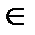V і довільному дійсному α:

A (х + у, z) = A (х, z) + A (y, z);

A (α х, y) = αA (х, у);

A (z, х + у) = A (z, х) + A (z, y);

A (х, α y) = αA (х, у)

Ранг матриці білінійної форми не залежить від вибору базису і може бути названий тому рангом білінійної форми.

Білінійна форма називається симетричною, якщо x, y, 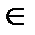V:

A (х, у) = A (y, x).

У цьому випадку a_ij = a_ji, тобто матриця [ a_ij ] симетричної білінійної форми в довільному базисі буде симетричною.

Якщо в симетричній білінійній формі A (х, у) покласти х = у, то отримається квадратична форма А (х, х). Із квадратичної форми однозначно визначається і відповідна їй симетрична білінійна форма.

Білінійна функція називається кососиметричною, якщо

x, y, 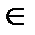V: A (х, у) = - A (y, x).

Дата добавления: 2015-10-29