Властивості z-перетворення

Поняття про імпульсні динамічні об’єкти

Імпульсні динамічні об’єкти являють собою особливий клас об’єктів, у яких вихідна величина одного чи декількох елементів має дискретний характер, тобто являє собою послідовність імпульсів. Зміна якого-небудь параметра імпульсів у залежності від вхідного сигналу називається модуляцією імпульсів вхідним сигналом, а пристрій, що формує послідовність модульованих імпульсів, називається імпульсним елементом.

Відмітимо, що імпульсні динамічні об’єкти, як і динамічні об’єкти неперервної дії, можуть бути лінійними і нелінійними. Ми будемо розглядати тільки лінійні імпульсні динамічні об’єкти, тобто такі, для яких можна застосувати принцип суперпозиції, де, в даному випадку, вхідні або вихідні сигнали або ж і ті і інші є імпульсними функціями.

Дискретне перетворення Лапласа

Для дослідження розв’язків різницевих рівнянь у загальному вигляді широко використовується дискретне перетворення Лапласа — аналог раніше розглянутого перетворення Лапласа для неперервних оригіналів.

Дискретне перетворення Лапласа визначається формулою:

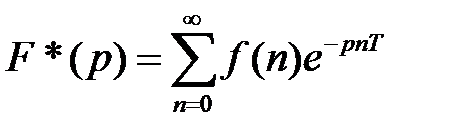. (1)

У цій формулі, як і у випадку неперервного перетворення Лапласа, комплексна величина p=σ+iω, де σ > c — абсциси абсолютної збіжності. При σ₀< 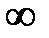ряд, обумовлений формулою (1), сходиться і ґратчастій функції відповідає деяке зображення

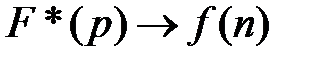, (2)

чи

F* (p)= L [ f (n)]. (3)

Z-перетворення і його властивості

Для дослідження імпульсних динамічних об’єктів велике поширення одержало z-перетворення, тісно зв'язане з дискретним перетворенням Лапласа.

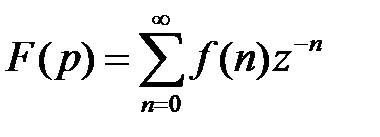. (4)

Функція F (z) називається z-перетворенням (зображенням) ґратчастої функції f (n) (оригіналу). Символи Z { f (n)} і Z ^–1{ f (n)}, відповідно, позначають операції прямого і зворотного z- перетворення. Ці операції часто записуються також у вигляді

F(z) 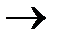f(n).

Властивості z-перетворення

Ці властивості багато в чому аналогічні властивостям перетворення Лапласа. Перелічимо деякі з них.

1. Лінійність. Якщо 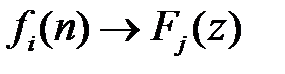, то для

маємо

.

2. Запізнювання. Якщо 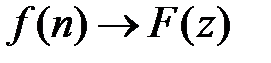і , то .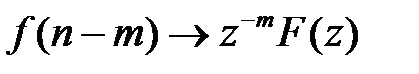

3. Зсув зображення. Якщо , то

4. Зображення різниць. Якщо 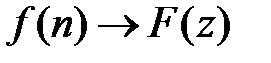і f(—n)=0, то

.

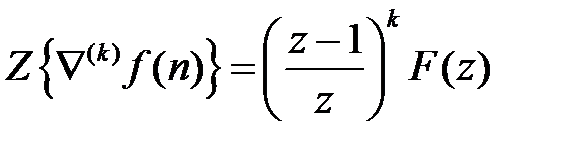Відмітимо, що при (неперервний випадок) множник у правій частині прямує до границі:

.

5. Зображення сум. Якщ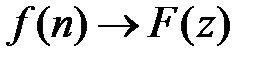о , то

.

У таблиці 1 приведені деякі зображення F (z) і F (p) — перетворення Лапласа оригіналів, які найчастіше зустрічаються.

Таблиця 1

Неперервний сигнал	Перетворення Лапласа	z-перетворення
u (t)   t 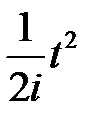    e ^–αt   sin βt   cos βt   e ^– αtsin βt   e ^– αtcos βt

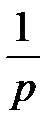
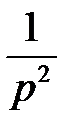
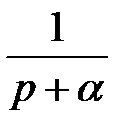
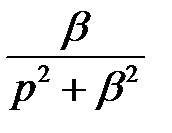
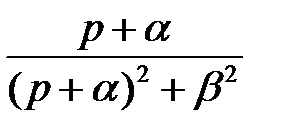
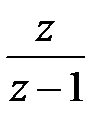
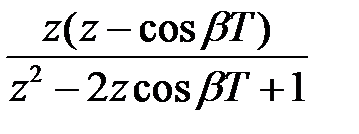
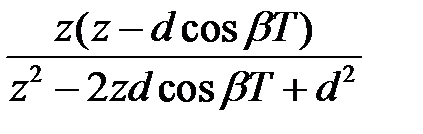
Використовуючи вищенаведені властивості, ми можемо застосувати z -перетворення до розв’язку різницевих рівнянь.

Розглянемо найбільш цікавий випадок розв’язування різницевого рівняння

a ₀ y (n) +a ₁ y (n –1) +…+a_m y (n – m) =b ₀ f (n) +b ₁ f (n –1) +…+b _l f (n –1), (5)

коли шукана ґратчаста функція до моменту часу п = 0 тотожно дорівнює нулю і, крім того, функція f (п) у правій частині (5) діє в момент часу n = 0. Вважаючи, що

y (n) Y (z), f (n) F (z)

і застосовуючи z-перетворення до обох частин рівняння (5), одержимо

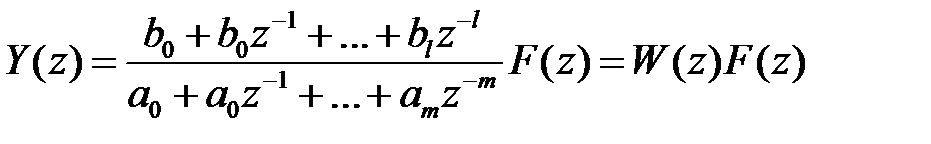. (6)

Введена тут дискретна передатна функція W (z)є аналогом передатної функції W (р). Дискретна передатна функція відіграє таку ж роль в імпульсних динамічних об’єктів, як і звичайна передатна функція в неперервних системах.

Знаходження оригіналу функції за її z-перетворенням є знаходженням

.

Зазвичай, z-зображення ґратчастої функції можна представити як відношення двох поліномів:

. (7)

Обмежимося випадком, коли степінь полінома Q (z) більше степеня полінома zР (z) і рівняння

Q (z) =0, (8)

має k різних ненульових коренів z_j, причому k є степенем полінома Q (z). Тоді зображення (7) представимо у вигляді суми

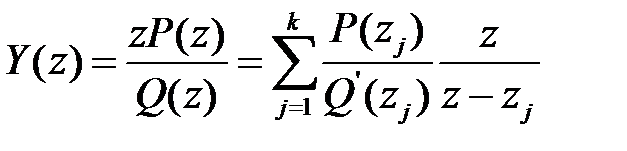. (9)

Елементарному виразу 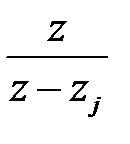, відповідно до таблиці 1, відповідає оригінал

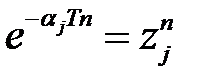, (10)

де

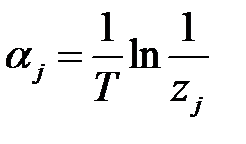. (11)

Тому оригінал у (п) =Z ^–1{ Y (z)} буде дорівнювати

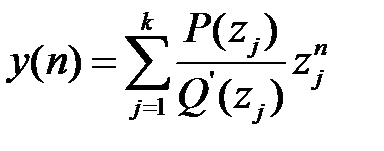. (12)

Розглянемо приклад чисельної реалізації математичної моделі динамічного об'єкту, який заданий передатною функцією

. (13)

Приведемо її до табличного вигляду

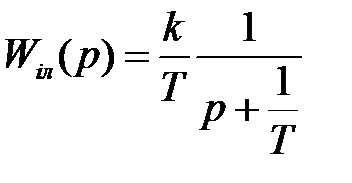. (14)

Згідно таблиці в оригіналах їй відповідає вагова функція

. (15)

З врахуванням

Y (p) =W (p) X (p)(16)

із (15) в зображеннях отримаємо рівняння

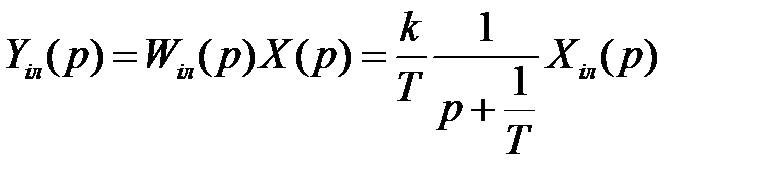, (17)

яке зв’язує зображення вхідного X_іл (p) і вихідного Y_іл (p) сигналів інерційної ланки. Від (17) перейдемо до оригіналів.

Враховуючи, що добутку двох функцій зображень (W_іл (p)і X_іл (p)) відповідає згортка їх оригіналів, отримуємо

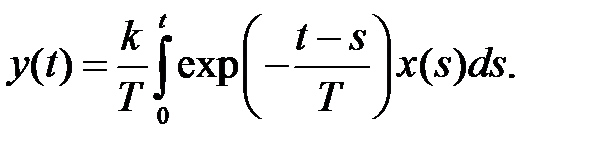(18)

В (17) дискретизуємо час t = nh, інтеграл апроксимуємо квадратурною сумою з квадратурними коефіцієнтами, які реалізують формулу правих прямокутників

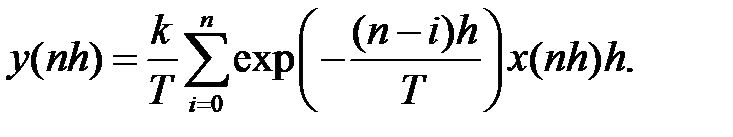(19)

Використовуючи те, що дискретній згортці двох градчатих функцій-оригіналів відповідає добуток двох функцій в Z-перетворенні

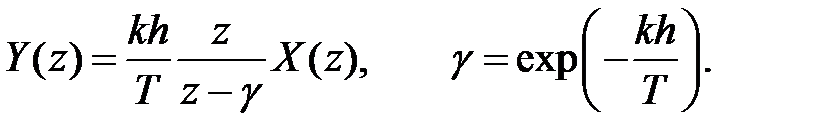(20)

Вираз (20) має структуру типу (16), і в ній можна визначити фрагмент, який можна назвати дискретною передатною функцією

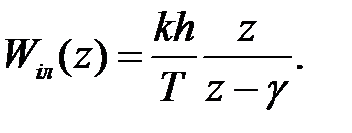(21)

Вираз (20) перетворимо до вигляду

від якого з використанням теореми про зсув можна легко перейти до оригіналів (множення функції-зображення на z^–n є зсув на n кроків аргументу функції-оригіналу)

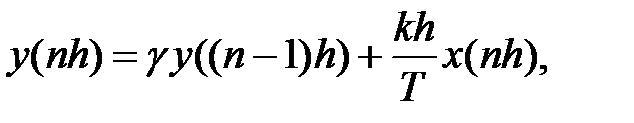
що можна назвати різницевим рівнянням

(22)

Дата добавления: 2015-10-30